13

I am a math newbie, but I stumbled across this while I was working on a game in python. This is the proof I have, I believe it shows that the halfway point between $0$ and infinity is $1$:

test

If it is true, I'm probably not the first to figure this out, but even still, I just want some kind of confirmation. This is very mind blowing for me right now :D

Stella Biderman
  • 31,155
talha tariq
  • 217
  • 7
    The linked image describes lines with slopes $0,1,\infty$ respectively. These lines pictured are specifically the lines $y=0, y=x, x=0$ respectively. The line $y=1$ does not look like that. Regardless, it depends on what you mean by the "halfway point." Yes, the halfway point between $0^\circ$ and $90^\circ$ is $45^\circ$, but this doesn't mean much for the usual notions of halfway points between numbers on the real line. – JMoravitz Dec 24 '16 at 17:29
  • The "halfway point' between $a$ and $b$, one might define as $\frac{a+b}{2}$, for example the halfway point between $1$ and $3$ is $\frac{1+3}{2}=\frac{4}{2}=2$. Similarly the halfway point between $1$ and $101$ is $51$. Using this definition of halfway point, we can say the halfway point between $0$ and $x$ is $\frac{0+x}{2}$. Taking the limit as $x$ approaches infinity we have the "halfway point between 0 and infinity" is $\lim\limits_{x\to\infty}\frac{0+x}{2}$ which is larger than any real number, i.e. it diverges to $\infty$. – JMoravitz Dec 24 '16 at 17:33
  • 1
    This image certainly does not mean $1$ is the midpoint between $0$ and $\infty$ in the traditional sense. But math is all about exploration: we could define the distance between numbers $a,b$ as the angle between $y=ax$ and $y=bx$. Is this a particularly useful, or widely accepted definition? No. But one could still do it! Math is about exploration. The $p$-adic numbers famously arise from thinking about a different notion of distance for the rationals. – eepperly16 Dec 24 '16 at 17:39
  • 3
    In other words... it is well known that the halfway point between 0 and infinity is 42. – Did Dec 24 '16 at 17:52
  • 11
    I don't agree with the down votes on this question. The OP has put effort into thinking about the problem, and it is clear what the question is. A question being naive doesn't make it a bad question. – wgrenard Dec 24 '16 at 18:22
  • 3
    @wgrenard I agree with wgrend. I never understand mentality of people on this site, that day a very basic question got a lot of votes and hell, this question is not very different from http://math.stackexchange.com/questions/12906/is-value-of-pi-4, which is one of the top ten top voted questions of all time. –  Dec 24 '16 at 18:53
  • 3
    By the same argument, the halfway point between $0$ and infinity is $-1$. One context in which this makes sense is that of cross-ratios in projective geometry; the pair $(0,\infty)$ is harmonically divided by the pair $(1,-1)$, see also Wikipedia – Servaes Dec 24 '16 at 19:26
  • 1
    Well, I guess there are many answerers who have torn apart the original question in order to fabricate a question so they can answer it, and justify their answers. This is an example where it's become mostly become about the answerers and their choice approaches, and the initial question is never corrected, clarified, or answered. – amWhy Dec 24 '16 at 19:47
  • All these answers going ham on some university level mathematics. Maybe a simple answer would be nice too? – gowrath Dec 24 '16 at 22:42
  • Occam's razor seems not in favour with the crowd. – mvw Dec 24 '16 at 22:47
  • Infinity is not a number. – pshmath0 Dec 25 '16 at 00:41

7 Answers7

12

While I personally would not use the word "halfway", I don't find it totally unreasonable to say that 1 is in some sort of special position between $0$ and $\infty$. The sense I'm thinking of is that in the projective line (Wikipedia), over $\mathbb{R}$ or $\mathbb{C}$, the map $z\mapsto\frac{1}{z}$ flips all the numbers "below" $1$ to all the numbers "above" $1$ and vice versa (in particular, swapping $0$ and $\infty$), while fixing $1$.

Added: You can think of the projective line over $\mathbb{R}$ as a way of describing or capturing all the possible "slopes of lines" in the plane as a single mathematical object, and this object has a "symmetry" $z\mapsto \frac{1}{z}$ which makes $1$ stand out (though note that $-1$ stands out just as much). This directly relates to the idea behind your diagram, since you labeled your diagram with the slopes of the lines (the equations you wrote are incorrect though, as others have already pointed out.)

With regards to the projective line over $\mathbb{C}$, a.k.a. the Riemann sphere (Wikipedia), this is often manifested in illustrations as choosing the unit circle to be the "equator" between the "north pole" $\infty$ and "south pole" $0$. Here's the picture from Wikipedia:

enter image description here

(Of course, one can question to what extent the map $z\mapsto \frac{1}{z}$ is special.)

Zev Chonoles
  • 129,973
  • 4
    If course, the map $\frac{2}{z}$ does the same thing, but fixing$\sqrt{2}$. – Thomas Andrews Dec 24 '16 at 17:50
  • 2
    Of course. I'm not sure if there is a precise sense in which $\frac{1}{z}$ is more natural than $\frac{2}{z}$, though it feels so to me. – Zev Chonoles Dec 24 '16 at 18:14
  • I meant to upvote this and now see that I downvoted this. If you edit it, I'll happily change my vote. In terms of your question... Maybe in terms of giving the image of the natural numbers the "right spacing"? – Stella Biderman Dec 24 '16 at 18:58
  • 1
    Another attempt to look for a possible scenario which justifies an unreasonable result, – mvw Dec 24 '16 at 19:00
  • Amen, @mvw Ultimately, the answers are at best, not helpful, and at worst, confuse the OP, perhaps even damaging to the OP's learning. – amWhy Dec 24 '16 at 19:33
  • @StellaBiderman: I see, thanks for letting me know! I've made some edits now. Your explanation with regards to $\frac{1}{z}$ seems plausible, though I'd like it even more if there were something special about $\frac{1}{z}$ as an element in $\mathbb{C}(z)$ or $\mathrm{PGL}_2(\mathbb{C})$. – Zev Chonoles Dec 24 '16 at 19:36
  • 3
    @mwv The result is not at all unreasonable. In projective geometry the idea of the harmonically conjugate pairs of pairs of points generalizes the idea of the midpoint of a pair of points. The pairs $(0,\infty)$ and $(1,-1)$ are harmonically conjugate pairs, and this is so exactly for the reason that the picture in the question illustrates. Of course the wording in the question is very vague and imprecise, but there's an idea here, an idea that mathematicians have studied and documented. And they have come to a similar result. – Servaes Dec 24 '16 at 19:56
  • 1
    @Servaes Do you think this is a meaningful answer to an OP who is confusing lines with their slopes? (let alone complex numbers, let alone projective geometry!) At the very least, the answerer could have provided a disclaimer at the very beginning: *NOTE: This isn't really an answer to the OPs given question, but using mathematics beyond the OPs understanding, we can see that the Idea behind what I am projecting to be the question I'd like to answer....) is reasonable.* – amWhy Dec 24 '16 at 20:02
  • 2
    @Amwhy Yes, in part I do. Points on the real projective line correspond precisely to slopes of these lines in the plane, including the $y$-axis with 'infinite slope'. I do agree that the complex part is irrelevant here. I'll write up an answer of my own soon. – Servaes Dec 24 '16 at 20:08
  • 2
    @Servaes The use of "mind blowing" indicates that OP noticed that his result is at least counter intuitive. There is that certain urge to go the extra dimension or fringe metric that makes mathematicians vulnerable to that kind of possible trolling. – mvw Dec 24 '16 at 20:09
  • @mvw You're not being trolled until you think about it. – Servaes Dec 24 '16 at 20:10
  • 1
    @Servaes Trolli soit qui mal y pense. – mvw Dec 24 '16 at 20:11
  • 1
    @mvw I pity you for misunderstanding having your "mind blown" with missing simple concepts. Yes, the OP is not an educated math person, but a flash of insight motivated his question and every posted answer is teaching them the conditions in which they're right. –  Dec 24 '16 at 20:18
  • 1
    What I hate most is when an answerer fails to explain too the OP how their answer may be relevant to them. Offering insights from various perspectives may be entertaining to other answerers, but unless there is a connection (made explicit by the answerer) from the original question, to the given answer, and then back to how it applies to the OPs situation, there's no point in anyone ever asking a question! – amWhy Dec 24 '16 at 20:55
  • @mvw You missed my point entirely, and this thread is also becoming a waste of my time. –  Dec 24 '16 at 20:56
10

This is implicit in existing answers and comments but doesn't appear to have been said outright: What you've found is not that $1$ is halfway between $0$ and $\infty$, but that $\arctan(1) = \frac{\pi}{4}$ is halfway between $\arctan(0) = 0$ and $\arctan(\infty) = \frac{\pi}{2}$, the latter being viewed either as the limiting value, or as coming from the unique continuous extension of $\arctan$ to the extended reals.

In other words, $$ \int_{0}^{\infty} \frac{dx}{1 + x^{2}} = \int_{0}^{1} \frac{dx}{1 + x^{2}} + \int_{1}^{\infty} \frac{dx}{1 + x^{2}}, $$ and the two integrals on the right are equal.

Andrew D. Hwang
  • 78,195
8

I think the existing answers miss a bit of nuance: how do you define distance.

There are many different "distance functions" that you can define on the (extended) real numbers. The most commonly used one (which is usually presumed unless otherwise specified) is $d(x,y)=|x-y|$. Clearly under that notion of distance, $1$ is the midway point between $0$ and $2$, not $0$ and $\infty$.

Wikipedia gives some good information on distance functions (also known as metrics) which are defined to have the following properties:

1) $d(x,y) \geq 0$

2) $d(x,y)=0\iff x=y$

3) $d(x,y) = d(y,x)$

4) $d(x,y) + d(y,z) \geq d(x,z)$

This last property is known as the Triangle Inequality and is extremely important to many applications of metrics and theorems about metric spaces (which are just sets on which one can define a metric). Some examples of metrics on $\mathbb{R}$ include $d(x,y)=\max(1,|x-y|)$, $d(x,y) = (x-y)^2$, and the function that is $1$ when $x\neq y$ and $0$ when $x=y$.

When you use terms like "half way" you need to specify which metric you are using. The "usual" metric on $\mathbb{R}$ is $d(x,y)=|x-y|$ where this property obviously doesn't hold. But there are metrics on $\mathbb{R}\cup\{\infty\}$ for which $1$ is half way between $0$ and $\infty$. Try to come up with an example based on your picture! Then try to come up with a different example based on the picture in Zev's answer.

These lecture notes talk about metric spaces in general and prove some cool theorems about them.

Stella Biderman
  • 31,155
  • 2
    If not otherwise stated the standard Euclidean metric applies. So using "half way" is perfectly fine. – mvw Dec 24 '16 at 18:24
2

From your picture, you might just as well say that the halfway point between $0$ and infinity is $-1$... In projective geometry your idea can be made precise, but this requires some technical background. I won't elaborate on that here, but here's a nice (corollary of) a result from projective geometry:

For the pair of lines in the plane with slopes $0$ and $\infty$, the pair of lines with slopes $1$ and $-1$ is the unique other pair with the following property: Every line parallel to one of these four lines intersects the lines in three points, and one of them is halfway inbetween the other two.

In this sense both $1$ and $-1$ are 'halfway between' $0$ and infinity; there's infinity in both directions ;) Much stronger and prettier results than the above actually hold, but they require more theory. If you're interested look up some projective geometry, in particular:

I can also recommend the book Classical Geometry - Euclidean, Transformational, Inversive, and Projective by I.E. Leonard, J.E. Lewis, A.C.F. Liu and G.W. Tokarsky. Chapter 13 and especially 14 make your intuition precise.

Servaes
  • 63,261
  • 7
  • 75
  • 163
2

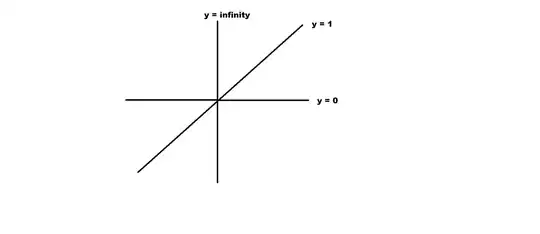
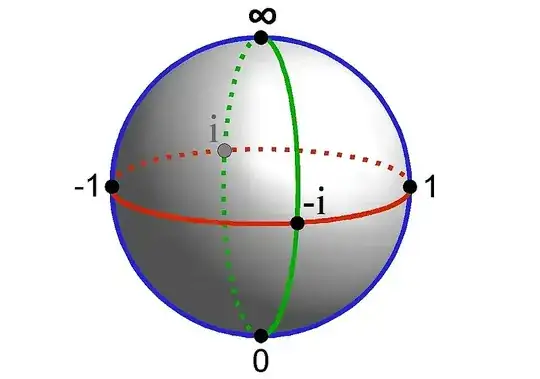
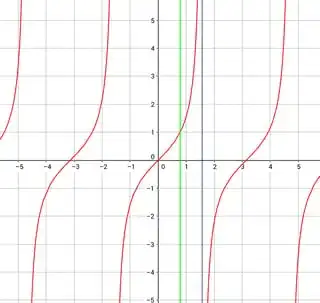
Another notion where 1 could be seen as "halfway" between 0 and +infinity is the Farey sequence:

$$ F_1 = { \frac 0 1, \frac 1 1 } $$ $$ F_2 = { \frac 0 1, \frac 1 2, \frac 1 1 } $$ $$ F_3 = { \frac 0 1, \frac 1 3, \frac 1 2, \frac 2 3, \frac 1 1 } $$

If we try to extend it from $(0,1)$ to $(0, +\infty)$, the simplest solution is to start from:

$$ E_0 = { \frac 0 1, \frac 1 0 } $$ and we get the extended sequence, where every term has all the fractions of the original term and their symmetrical fractions:: $$ E_1 = { \frac 0 1, \frac 1 1, \frac 1 0 } $$ $$ E_2 = { \frac 0 1, \frac 1 2, \frac 1 1, \frac 2 1, \frac 1 0 } $$ $$ E_3 = { \frac 0 1, \frac 1 3, \frac 1 2, \frac 2 3, \frac 1 1, \frac 3 2, \frac 2 1, \frac 3 1, \frac 1 0 } $$

ypercubeᵀᴹ
  • 936
1

By the same reasoning, the tangent of $22.5^\circ$ would be "halfway" between zero and $1$. That's $\tan 22.5^\circ = \sqrt{2}-1$.

It might be more exact to say "the slope $1$ is halfway between the slope $\infty$ and the slope $0$." Of course, the slope $-1$ is halfway between these two, too, so in the end, it is a probably a bit useless.

For example, what is "halfway between $0$ and $4$? Why is that larger than halfway between $0$ and $\infty$?

We can say a lot of things, as long as we define what we mean in a non-contradictory way. The question is always "does this definition have any use to us?" It probably doesn't - to the extent we need it, it is really "halfway between" two angles, not $0$ and $\infty$.

This particular "halfway between" definition would keep "between" from following one of these rules:

  • The number halfway between $a$ and $b$ is between $a$ and $b$
  • If $a<b<c$ then the number halfway between $a$ and $c$ is less than the number halfway between $b$ and $c$.
  • Every positive real is between $0$ and $\infty$.

So now, whenever you talk about "the number(s) halfway between $a$ and $b$" you have be careful to exclude $\infty$, or you'd have to avoid using one or more of the above properties.

Thomas Andrews
  • 177,126
-1

Short answer:

No, $1$ is the halfway point between $0$ and $2$.
The halfway point between $0$ and infinity is infinity.
(Unless you want to model a non-Euclidean world)

Long answer:

No, the image gives the values for $y'(x) = m$ of some lines $y(x) = m x$, not the values for $y(x)$.

This value $m$ is not linear dependent on the angle $\alpha$ of the line $y(x)$ with the positive $x$-axis:

$$ m = \tan \alpha $$ graph

Your pick is the value at the mid angle $\pi/4$ (green line).

It is indeed in the middle of the $\alpha$ interval $[0,\pi/2]$ (the blue line is $x=\pi/2$), but not a good pick for a middle value of $y'$ between $\alpha=0, y'=m=0$ and $\alpha=\pi/2, y'=m=\infty$. Almost all value of $y'$ is in the right half of the interval, in $[\pi/4,\pi/2]$.

Here the average is better suited.

In fact over the angles from $0$ to $\pi/2$ the average is $$ \overline{y'} = \frac{\int\limits_0^{\pi/2}\tan \alpha\,d\alpha}{\int\limits_0^{\pi/2} d\alpha} = \frac 2 \pi \left[ -\ln \lvert \cos \alpha \rvert \vphantom{\frac11} \right]_{\alpha=0}^{\alpha\to \pi/2} \to \infty $$ as expected.

mvw
  • 34,562