9

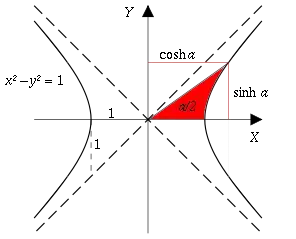
From what I know, the hyperbolic trigonometric functions are almost the same as the circular trigonometric functions ($\sin, \cos, \tan$, et cetera without the $h$ suffix), except they output when a line coming from the centre at the given angle hits the surface of a hyperbola, rather than a circle.

From what I've seen, the relevant hyperbola has asymptotes at $45^\circ$, $-135^\circ$, $225^\circ$, and $315^\circ$, so basically the lines $y = 0$ and $x = 0$, but rotated $45^\circ$. This means that a line told to go along any of these asymptotes — defined by the fact that the hyperbola will never meet them — surely will never meet the hyperbola because it basically is the asymptote!?

And anywhere that goes through, judging by the diagrams I've looked at on-line, the empty space above and below the origin (excluding where the hyperbola really is,) should, as well, surely be infinity, since it never gets to the hyperbola?

The summarised question: How come giving a hyperbolic function that treads along the asymptotes does not give infinity or some other undefined answer?

Asaf Karagila
  • 393,674
Tachytaenius
  • 252
  • 1
  • 9

2 Answers2

31

Because the argument to the hyperbolic trigonometric functions is not the angle that your line makes with the $x$-axis, but rather the area between your line, the $x$-axis and the hyperbola (although to be more exact, with the $a/2$ in the picture, it's the area between your line, its reflection across the $x$-axis, and the hyperbola, with a sign to differentiate between the two sides of the $x$-axis). See the image below:

enter image description here

Note that you could say that the regular sine and cosine functions do the same thing, taking in the area of a sector of the unit circle, so it is actually the same, in a way.

Arthur
  • 199,419
  • "Note that you could argue that the regular sine and cosine functions do the same thing, taking in the area of a sector of the unit circle, so it is actually the same, in a way." Confuses me, because from what I have seen the circular sine, cosine and such ARE given an angle, not an area. So... sin isn't so similar to sinh after all? – Tachytaenius Dec 22 '16 at 18:37
  • 8
    @wolfboyft What I'm saying is that while sine and cosine are usually defined using angles, there is nothing wrong in deciding that they're defined from the area instead. That would make their connection to the hyperbolic functions a bit clearer, although their connection to right-angled triangles would be a bit less so. – Arthur Dec 22 '16 at 18:41
  • 2
    Alternatively, one can define sine/cosine in terms of the arc length subtended; that line of thinking leads to elliptic functions when applied to conic sections. – Semiclassical Dec 22 '16 at 18:56
  • 2
    @wolfboyft Provided the angle is given in radians and radius of circle is 1, the area of sector with angle α equals to α/2 (so, full circle is π - πr^2) – Swift Dec 22 '16 at 20:02
2

The hyperbolic trig functions aren't defined by the angle turned off the $x$-axis, but by the area between the hyperbola and the line at angle $\theta.$ There is infinite area between the asymptote and the curve, so as $\theta$ goes from $0$ to $45$ degrees, the area goes from $0$ to infinity. It's the area that's plugged into the function, not the angle. While typing I see that Arthur has answered with a diagram. That's a good diagram. As the red area goes to infinity, the angle goes to $45$ degrees, but $\sinh( \mbox{area} )$ is the $y$-coordinate of the intersection point. It goes to infinity with the area.

B. Goddard
  • 1