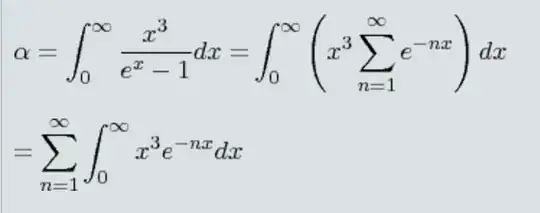0

I am exploring a famous definite integral that is critical to the Blackbody radiation problem. The solution to the integral is laid out in great detail here: http://www.sosmath.com/CBB/viewtopic.php?p=67530

I understand every point proffered by the poster except one. How can the order of the discrete sum operator and the Integral operator be exchange without breaking the equivalence relation? Considering that both operators are linear operators, I can intuit that order may not matter. However, the fact that the Sigma operator sums over discrete quantities while the Integral sums continuously over infinitesimal quantities causes me to doubt whether the order of both operators can be exchanged while maintaining equality. Time constraints force me to accept on faith that this is true but I am eager to look into the validity of this. Can anyone point me to some mathematical sources that will elucidate this matter? Thank You.Integral Example

H3G3moKnight
  • 85
  • They are summing/integrating over different variables so it doesn't matter... try writing it out with just two terms. Because they're both linear operators, it works fine either direction. – DilithiumMatrix Dec 20 '16 at 03:50
  • Wonderful, I do believe that this holds the answer. – H3G3moKnight Dec 20 '16 at 08:20
  • @DilithiumMatrix I strongly disagree. Take a look at this question (and its answers). – Antoine Dec 20 '16 at 13:03
  • @Antoine I don't see any disagreement in that question... sure if the sum or integrand is not well defined (i.e. not convergent) then okay, maybe it doesn't work --- but then it wouldn't really matter anyway in this context. – DilithiumMatrix Dec 20 '16 at 18:58
  • @DilithiumMatrix Sum and integral are always "summing/integrating over different varaiables", so this cannot be an argument for interchangeability of $\int$ and $\sum$. – Antoine Dec 21 '16 at 09:32

0 Answers0