40

recent conjecture ：Let $S_n=1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}$, where $n$ is a positive integer. Prove that ：there exist infinite many $n\in\mathbb{N^{+}}$ such that $$S_n-[S_n]<\dfrac{1}{n^2}$$ where $[x]$ represents the largest integer not exceeding $x$.

previous problem:How to prove that $a<S_n-[S_n]<b$ infinitely often

Community
  • 1
math110
  • 93,304
  • 4
    Can you find any example with $n \gt 1$? Having looked at this for small $n$, I would guess there are probably no other examples. – Henry Dec 18 '16 at 01:33
  • @Henry: do you mean examples other than 1? [I didn't find any small $n.$] – coffeemath Dec 18 '16 at 01:35
  • @coffeemath: yes: $1$ is an example because $S_1$ is an integer. But then the possibilities shrink geometrically or exponentially and so have a small sum beyond the values I can test in the precision limit of my machine – Henry Dec 18 '16 at 01:39
  • 10
    Heuristically this should happen a finite number of times. Consider the values $n_i$ where $\lfloor H_{n_i}\rfloor $ jumps from $i$ to $i+1$. Since $H_i\approx\ln i$, we have $n_i\approx e^i$ (this is of course a very rough approximation, but that's all we need for this heuristic). Now, at $n_i$ it's reasonable to assume (heuristically) that the fractional part ${H_{n_i}}$ is equidistributed in $(0, \frac1{n_i})$; this means that the probability it's less than $1/(n_i^2)$ is $\frac1{n_i}$. But then the total number of 'hits' is $\sum_i(n_i^{-1})\approx\sum_i e^{-i}$, which converges. – Steven Stadnicki Dec 23 '16 at 02:07
  • @StevenStadnicki I don't have an intuition that suggests that ${H_n}$ is equidistributed in $(0, 1/n_i)$ (I haven't worked with equidistribution much, and never with something other than mod 1). Could you provide some intuition? – alphacapture Dec 23 '16 at 21:34
  • 1
    @alphacapture There's nothing specific about ${H_{n_i}}$ here - the heuristic is that we've added $1/n_i$ to $H_{n_i-1}$ to get a number that 'rolls over' into the next integer, so we know that ${H_{n_i}}\geq 0$ (by definition) and ${H_{n_i}}\leq 1/n_i$ (because otherwise the rollover point would've been earlier); the heuristic is just in the assertion it's equidistributed within its possible range (because we have no specific reason to believe otherwise). – Steven Stadnicki Dec 23 '16 at 23:25
  • 2
    Formally, we can say that the set ${\alpha \in [0,1] : (S_n+\alpha)-[S_n+\alpha] < 1/n^2 \ \text{for infinitely many} \ n \in \mathbb{N}^+}$ has measure $0$. But showing that $0$ does not belong to this set doesn't appear to be trivial. – JimmyK4542 Dec 24 '16 at 07:42
  • 1
    Article that might be useful: R. P. Boas, Jr. and J. W. Wrench, Jr., Partial Sums of the Harmonic Series, The American Mathematical Monthly. "Our problem is to compute the smallest integer $n = n_A$ for which $H_n$ exceeds a given number $A$" – Winther Jan 10 '17 at 08:46
  • 1
    @Winther: that would be $(4)$ from my answer. In that paper, they add $1$ and floor it to get the ceiling. – robjohn Jan 12 '17 at 09:56
  • 4
    You should probably add to your post that you have now asked the same question on [MathOverflow](there exist infinite many $n\in\mathbb{N}$ such that $S_n-[S_n]<\frac{1}{n^2}$). See this answer and other discussions about [meta-tag:cross-posting]. – Martin Sleziak Jan 15 '17 at 11:42
  • 1
    I have checked all $n$ up to $2\cdot10^{10}$ and there is no $n$ such the above inequality fulfilled in that range. – LRDPRDX Jan 20 '17 at 18:12
  • @Wolfgang However my calculation show there might be one solution up to $10^{100}$. – Takahiro Waki Jan 21 '17 at 06:23
  • Do you know exact value of $n$? – LRDPRDX Jan 21 '17 at 08:29
  • I calculated upperbound is 1/6, lowerbound is 1/9. This is of the expected number of solution. – Takahiro Waki Jan 21 '17 at 12:41
  • @TakahiroWaki, bound for what? – LRDPRDX Jan 22 '17 at 12:51
  • @Wolfgang This is the expected number of solution which the case is 1/n^2. I calculated that by hand before your answer. – Takahiro Waki Jan 22 '17 at 13:19
  • $n = 6$ or $n = 9?$. Unfortunately this are not answers because $$\Delta(S_n) = 0.45$$ and 0.82... respectively. – LRDPRDX Jan 23 '17 at 16:23
  • I've made a long answer with numerical tables at http://mathoverflow.net/a/260669/7710 – Gottfried Helms Jan 27 '17 at 22:24

2 Answers2

20

This is a heuristic argument. It does not show that there are not infinitely many occurrences, just that without some unforeseen conditions, the probability of infinitely many occurrences is zero.

The Euler-Maclaurin Sum Formula says that $$ H_n=\log(n)+\gamma+\frac1{2n}-\frac1{12n^2}+\frac1{120n^4}+O\!\left(\frac1{n^6}\right)\tag{1} $$ Subtracting $\gamma$ and exponentiating gives $$ \begin{align} e^{H_n-\gamma} &=ne^{\frac1{2n}-\frac1{12n^2}+\frac1{120n^4}}+O\!\left(\frac1{n^5}\right)\\ &=\left(\frac1n-\frac1{2n^2}+\frac5{24n^3}-\frac1{16n^4}+\frac{47}{5760n^5}+\frac1{2304n^6}\right)^{-1}+O\!\left(\frac1{n^5}\right)\tag{2} \end{align} $$ Inversion of the power series $y=x-\frac{x^2}2+\frac{5x^3}{24}-\frac{x^4}{16}+\frac{47x^5}{5760}+\frac{x^6}{2304}$ says $$ x=y+\frac{y^2}2+\frac{7y^3}{24}+\frac{y^4}6+\frac{523y^5}{5760}+\frac{y^6}{20}+O\!\left(y^7\right)\tag{3} $$ where $x=\frac1n$ and $y=e^{\gamma-H_n}$. Taking the reciprocal of $(3)$ yields $$ n=e^{H_n-\gamma}-\frac12-\frac1{24}e^{\gamma-H_n}+\frac3{640}e^{3\gamma-3H_n}+O\!\left(\frac1{n^5}\right)\tag{4} $$ To find an $n$ so that the fractional part of $H_n$ is less than $\frac1{n^2}$, we need to find an $H_n$ so that the fractional part of $n$ is greater than $1-\frac1n$. $$ \begin{array}{r|r} H_n&n\\\hline 1&1.000000000000\\ 2&3.638675849525\\ 3&10.773523676598\\ 4&30.153290055642\\ 5&82.827475640215\\ 6&226.008738099299\\ 7&615.215019121592\\ 8&1673.187107043897\\ 9&4549.053308117194 \end{array}\tag{5} $$ Without a reason that the fractional part of $(4)$ not be uniformly distributed, the probability that the fractional part of $H_n$ is less than $\frac1{n^2}$ would be $$ \frac1n\approx e^{\gamma-H_n}\tag{6} $$ and since $$ \begin{align} \sum_{H_n=1}^\infty e^{\gamma-H_n} &=\frac{e^\gamma}{e-1}\\ &\lt\infty\tag{7} \end{align} $$ Borel-Cantelli says that the probability that there are infinitely many $n$ so that the fractional part of $H_n$ is less than $\frac1{n^2}$ is $0$.

robjohn
  • 345,667
  • 1
    How much chance that the Pythagorean Theorem is true? I guess someone can give a probabilistic "proof" that it is zero too. – Han de Bruijn Jan 12 '17 at 20:13
  • 3
    I explicitly said that this was not a proof, that it was only heuristic. If someone posts a proof, this would serve to enhance the wonder because the odds are against it. If nothing else, the inverse of the harmonic numbers was worth the exercise for me. – robjohn Jan 12 '17 at 20:20
  • 1
    I hope that some of the results that I have gotten, while they don't settle the question, are helpful to someone. – robjohn Jan 12 '17 at 20:40
  • Sure Rob, but I only wanted to point out that one has to be careful with transfer of probabilistic arguments to environments where they do not really belong. – Han de Bruijn Jan 12 '17 at 20:59
  • Huh, How'd you invert the series? – Simply Beautiful Art Jan 17 '17 at 01:14
  • @SimpleArt: It's not too difficult if you work mod $x^2$ to get the coefficient of $x$. Then fixing that coefficient, work mod $x^3$ to get the coefficient of $x^2$. Then fixing those coefficients, work mod $x^4$ to get the coefficient of $x^3$. And so on. This algorithm is implemented in most CAS programs. – robjohn Jan 17 '17 at 02:11
  • Hm, interesting... – Simply Beautiful Art Jan 17 '17 at 12:24
  • @SimpleArt: as long as you can compose power series, which is much easier when there is no constant term. – robjohn Jan 17 '17 at 14:26
  • Related to your table $(5)$ is the set of $n$ values where the fractional part of $H_n$ jumps to the next integer. These are the $n$ where one would search for an example. See OEIS A002387 for some related comments. – Jeppe Stig Nielsen Jan 18 '17 at 11:05
  • @JeppeStigNielsen: Yes. – robjohn Jan 19 '17 at 15:11
  • 1
    @HandeBruijn Out of curiosity, how do you (propose to) cast the Pythagorean Theorem in such a form as to be able to apply probabilistic heuristics to it? – Steven Stadnicki Jan 20 '17 at 22:33
1

Sorry for posting as answer but I think it would be more convenient here. Firstly, I am offering to change the title of the question to ''There is no $n$ such ... ''. It might be more attractive. Secondly, I have the following generalized conjecture:

Let $M$ be the set of all $n$ such that $$H_n - \lfloor{H_n\rfloor} < \frac{1}{n^{1+\epsilon}}.$$ Then $$\forall\epsilon>0 : |M| = \bar\eta(\epsilon) < \infty.$$

Also I suspect that $\bar\eta$ monotonically decreasing function on $(0,1]$. Below I presented possible values of $\bar\eta$ ('possible' because I am not able to check all $n$'s). Actually, I was checking only up to $10^5$ first $n$'s.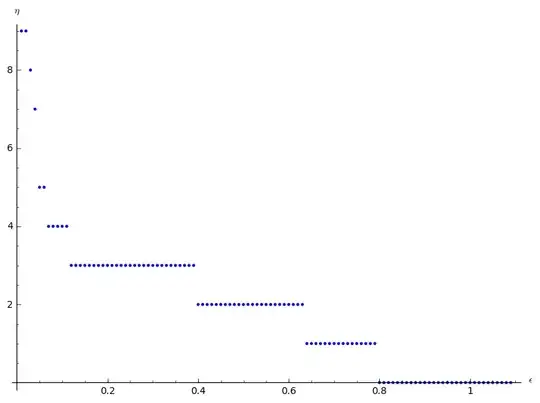points_eta Next, I tried all $n$'s up to $10^6$.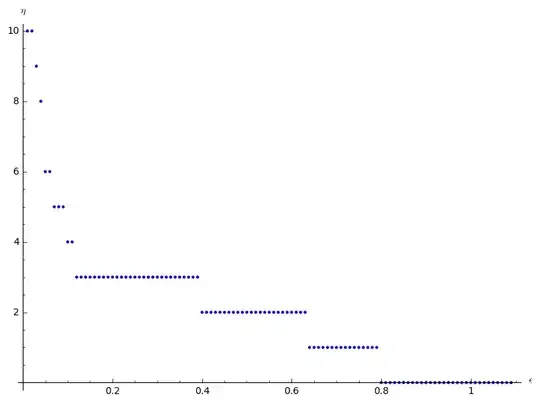points_eta6 Note that I assume $H_n$ starts with $\frac12$, not with 1.

LRDPRDX
  • 1,288