2

I have an integral $\int_D\,\frac{1}{x^2+y^2}dxdy$ which I should integrate over $D$.

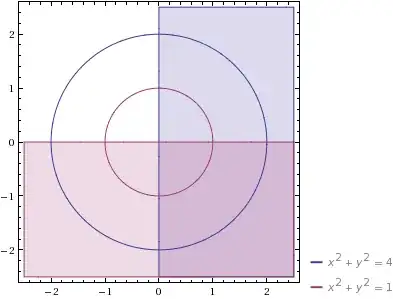
$D$ is limited by $1 \leq x^2 +y^2 \leq 4$ and $x \geq 0, y \leq 0$

I have plotted the limits and the integration should be between the circles in the down right quadrant. enter image description here

Update: after hint of polar coordinate, limits and that $r$ should be $\frac{1}{r}$:

$$\int_D\,\frac{1}{x^2+y^2}dxdy = \int_{\frac{3\pi}{2}}^{2\pi}\,\int_1^2{}\,\frac{1}{r}drd\theta$$

finally correct? :)

Américo Tavares
  • 38,602
  • 3
    Hint: Polar coordinates. – Alexander Thumm Oct 01 '12 at 21:14
  • 2
    Normally in polar coordinates, $\theta=0$ is the $x$ axis and angles are measured counterclockwise. The limits would then be $\frac {3\pi}2 \le \theta \le 2\pi$ – Ross Millikan Oct 01 '12 at 21:26
  • Thanks for the polar hint and very much thanks for the riminder that angels are going counter clockwise I had a smaler blackout it seems :) –  Oct 01 '12 at 21:38

1 Answers1

0

Hints:

$$\dfrac{1}{x^2+y^2}=\dfrac{1}{r^2}$$

$$\dfrac{1}{x^2+y^2}r=\dfrac{1}{r}$$

See this question.

ADDED. Your update is now correct: the integrand in polar coordinates becomes $1/r\;$ after the multiplication by $r$.

Community
  • 1
Américo Tavares
  • 38,602