3

For a circle with radius $r$, we have $\frac{dA}{dr}=\frac{d}{dr}\pi r^2=2\pi r=C$. But for an ellipse with $a=r$ and $b=2r$, $\frac{dA}{dr}=\frac{d}{dr}2\pi r^2=4\pi r\ne C$. Shouldn't the area of the ellipse change by its circumference?

W. Zhu
  • 1,325
  • As you are taking the values of a and b accurately. It is not the case. Also you can't find accurately the perimeter of an ellipse. I think the main reason is this. – Kanwaljit Singh Dec 11 '16 at 03:45

2 Answers2

1

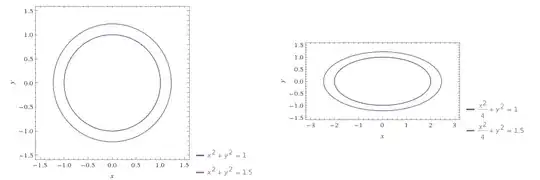
The reason why $\frac{dA}{dr}=C$ works for the circle is that (loosely speaking) increasing the radius by $dr$ adds a "stripe" of constant "width" around the circle, therefore the added area is (at the limit) proportional to $dr$. This does not happen for an ellipse, however, where the "stripe" becomes thicker around the endpoints of the longer axis, as can be seen in the drawings below.

dA/dr

For the full math behind this intuition, see for example this answer to Why is the derivative of a circle's area its perimeter (and similarly for spheres)?.

Community
  • 1
dxiv
  • 76,497
1

I recommend the article by J. Tong, Area and perimeter, volume and surface area, College Math. J. 28 (1) (1997) 57. He shows that for any region where the area can be written as $A(s)=cs^2$ and the perimeter as $L(s)=ks$, you can set $x=(2c/k)s$, and you will get $A′(x)=L(x)$. That means that by careful parametrization, the above holds for rectangles and ellipses, too.

Helmer.Aslaksen
  • 167