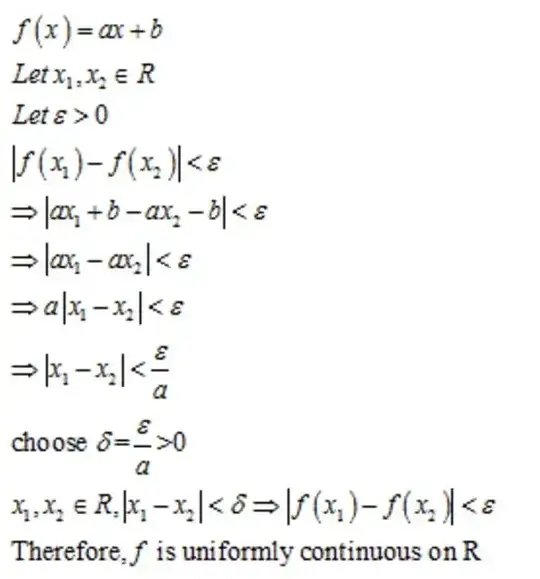Clearly, this problem requires applying epsilon, delta definition of uniform continuity. im having trouble finding values that will work here and hence, writing the proof in general.
Asked
Active
Viewed 2,224 times
0
-
7See the answers to this question. – Dietrich Burde Dec 10 '16 at 19:23
-
What have you tried so far? What criteria must be satisfied to have uniform continuity? You're a lot more likely to get help if you've shown that you've at least made an effort. – NNN Dec 10 '16 at 19:50
2 Answers
3
We say $f$ is uniformly continuous if
$ \forall \, \varepsilon > 0 \; \exists \, \delta > 0 \,$ such that $\forall x,y\in \mathbb{R}$ we have $|x-y|<\delta \Rightarrow |f(x) - f(y)| < \varepsilon$.
If $a=0$, then $|f(x)-f(y)| = |b-b| = 0 < \varepsilon$ for any $\varepsilon$, so any $\delta$ works.
Now let $\varepsilon>0$ and suppose $a \neq 0$. Let $\delta = \frac{\varepsilon}{|a|}$ and suppose $|x-y|<\delta$. Then
$$ |f(x) - f(y)| = |ax + b - (ay + b)| = |ax - ay| = |a||x-y| < |a|\delta = |a|\frac{\varepsilon}{|a|} = \varepsilon $$
and we're done.
ODF
- 1,590
0
I figured out two values that work but not sure if this proof makes sense here
Aggrawal Puja
- 183
-
Only problems: $a$ might be negative, in which case you want to divide by the absolute value, and $a$ might be zero, in which case you want a slightly different approach. – Ian Dec 10 '16 at 19:52
-
Should I use the absolute value of (a) here then? instead of just a? – Aggrawal Puja Dec 10 '16 at 19:53
-