Assume that $f(x)\geq 0$ for $0\le x<\infty$ and $\int_{0}^{\infty} f(x)\, dx<\infty$. Could we conclude that $\lim_{x\to\infty} f(x)=0$? My idea is that if we can find a counter example, then $f(x)$ must be an oscillating function in $x$. Any suggestion, idea, or comment is welcome, thanks!
-
1No, in fact $f$ can be unbounded. Think of some thin triangles with very small bases and very large heights marching out to infinity. – zhw. Dec 09 '16 at 18:14
-
Are these thin triangles with the same base and the same height? – LCH Dec 09 '16 at 18:28
-
1How could they be when the base is small and the height is large? – zhw. Dec 09 '16 at 18:31
2 Answers
No, you are right there is a counterexample.
Join the following dots: $$\left\{\left(n-\frac{1}{2^n},0\right),(n,1),\left(n+\frac{1}{2^n},0\right)\;:\;n\in\mathbb{N}^+\right\}.$$ and you will obtain the graph of a piecewise linear function with the desired property.
P.S. Here is an unbounded version: $$\left\{\left(n-\frac{1}{4^n},0\right),(n,2^n),\left(n+\frac{1}{4^n},0\right)\;:\;n\in\mathbb{N}^+\right\}. $$
- 145,942
-
-
1@LCH If you join the dots you obtain the graph of a piecewise linear function with the desired property – Robert Z Dec 09 '16 at 18:28
-
Thanks. For the first case, $\sum_{n=1}^{\infty} \frac{1}{2^n}=1$ but, $\lim_{n\to\infty} n\neq 0$, right? I'm curious how come you figure out such an elegant counterexample. – LCH Dec 09 '16 at 18:44
-
1@LCH Yes, we sum the areas of triangles of base $2/4^n$ and height $2^n$. It is unbounded because $2^n\to+\infty$. You can try to construct your own example. – Robert Z Dec 09 '16 at 18:45
-
You mean "You've voted for this as a useful comment"? I'm a new comer, thanks for the reminding! :) – LCH Dec 09 '16 at 18:53
Let $m\ge0$ and $n\gt2m+2$. Then $$ \begin{align} \int_0^\infty x^m\left(\frac{1+\cos(2\pi x)}2\right)^{x^n}\,\mathrm{d}x &=\sum_{k=0}^\infty\int_0^1(x+k)^m\left(\frac{1+\cos(2\pi(x+k))}2\right)^{(x+k)^n}\,\mathrm{d}x\\ &\le\sum_{k=0}^\infty(k+1)^m\int_0^1\left(\frac{1+\cos(2\pi x)}2\right)^{k^n}\,\mathrm{d}x\\ &=\sum_{k=0}^\infty(k+1)^m\int_0^1\cos^{2k^n}(\pi x)\,\mathrm{d}x\\ &=1+\sum_{k=1}^\infty(k+1)^m\frac1{4^{k^n}}\binom{2k^n}{k^n}\\ &\le1+\sum_{k=1}^\infty\frac{2^mk^m}{\sqrt{\pi k^n}}\\ &=1+\frac{2^m}{\sqrt\pi}\zeta\left(\frac n2-m\right) \end{align} $$ where we've used inequality $(10)$ from this answer.
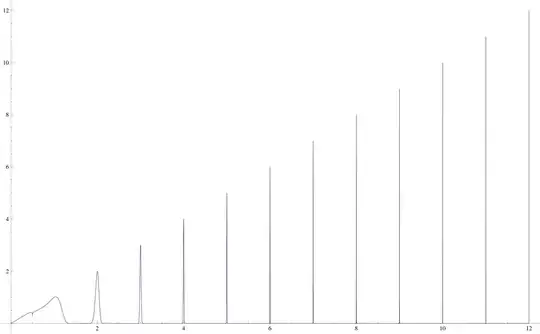
Thus, for $m\ge0$ and $n\gt2m+2$, $$ \int_0^\infty x^m\left(\frac{1+\cos(2\pi x)}2\right)^{x^n}\,\mathrm{d}x\lt\infty $$ However, for $x\in\mathbb{Z}$, we have $x^m\left(\frac{1+\cos(2\pi x)}2\right)^{x^n}=x^m$, so the function does not tend to $0$.
Here is the plot of this function for $m=1$ and $n=5$:
- 345,667