That is because the quantity $dx \ dy$ transforms to $r \ dr \ d\theta$ when you go from cartesian coordinates to polar coordinates.
The reason we get an extra "r" can be intuitively seen as follows:
in cartesian coordinates, $dx \ dy$ is our "unit of integration" (a small square). Similar to this,
in polar coordinates, our "unit of integration" is a "very thin band" which is of the form $dr \ dl$ where
$dr$ is the direction "outward" from the origin, and $dl$ is the small band. However, we know that $dl = r \ d\theta$
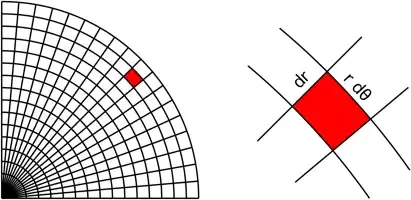
(from the usual arc-angle formula $l = r \theta$). Hence, our unit of integration will be
$$
dl \ dr = (r \ d \theta) \times dr = r \ dr \ d\theta
$$
However, this is only an intuitive approach which does not generalise (and can often be wrong). The correct way to do this is to
use something that is called as the Jacobian.
The Jacobian between two spaces represents in some sense the scaling factor of a "unit volume" from one space to another. So,
if we know the change in unit volume between two spaces, the new unit of integration becomes the old unit of integration multiplied
by this scaling factor.
$$
new = old \times jacobian
$$
The Jacobian is defined as the determinant of the matrix:
$$
J = \begin{bmatrix}\frac{dx_1}{dy_1} & \frac{dx_2}{dy_1} & \ldots & \frac{dx_n}{dy_1} \\
\cdots \\
\frac{dx_1}{dy_m} & \frac{dx_2}{dy_m} & \ldots & \frac{dx_n}{dy_m}
\end{bmatrix}
$$
where $x_i$ is the variables in the space you are "from" and the $y_i$ are the variables in the space you are "going to".
For us, we are "from" the Cartesian space and we are "going to" the Polar space. Hence,
$$
x_i = \{x, y\} \\
y_i = \{r, \theta\}
$$
We need to know how to differentiate the former with respect to the latter.
Since we know the relations
$$
x = r \cos \theta \\
y = r \sin \theta
$$
The Jacobian matrix becomes
$$
J = \begin{bmatrix}
\frac{dx}{dr} & \frac{dx}{d\theta} \\
\frac{dy}{dr} & \frac{dy}{d\theta} \\
\end{bmatrix} = \\
\begin{bmatrix}
\frac{r \cos \theta}{dr} & \frac{r \cos \theta}{d\theta} \\
\frac{r \sin \theta}{dr} & \frac{r \sin \theta}{d\theta} \\
\end{bmatrix} = \\
\begin{bmatrix}
\cos \theta & - r \sin \theta \\
\sin \theta & r \cos \theta \\
\end{bmatrix}
$$
The determinant of this matrix is
$$
|J| = (\cos \theta)(r \cos \theta) - (\sin \theta)(- r \sin \theta) \\
= r \cos^2 \theta+ r \sin^2 \theta = r
$$
Hence, to go from $dx dy$ to $dr d\theta$, we need to multiply by a factor of $r$. So the total transform is
$$
dx \ dy \rightarrow r \ dr \ d\theta
$$
The reason the Jacobian $J$ represents the increase in volume is because a determinant of a matrix gives us the volume of the
parallelopiped with the sides as the columns of the matrix. Here, our sides are of the form
$$
v_i = \begin{bmatrix}
\frac{dx}{dy_1} \\
\frac{dx}{dy_2} \\
\frac{dx}{dy_3} \\
\ldots
\frac{dx}{dy_n}
\end{bmatrix}
$$
which is the change of our dimension $x_i$ in the "new space". So, our total change will be the size of the volume change from the
old space to the new space.
