2

I found this interesting function defined by the following infinite series:

$$g(x)=\sum_{n=0}^\infty(-1)^nx^{2^n}$$

And I noticed that it followed the functional equation $g(x)=1-g(x^2)$. I was interested, particularly, in the following limit:

$$L=\lim_{x\to1^-}g(x)$$

And assuming it exists, the functional equation yields

$$L=1-L\implies L=\frac12$$

Which, at first look, the limit appears to exist.

enter image description here

However, upon closer inspection, convergence gets a little sketchy...

enter image description here

Can we determine if the limit converges?

Simply Beautiful Art
  • 74,685
  • 5
    It didn't converge, see answers of this. BTW, the functional equation should be $g(x) = x - g(x^2)$. – achille hui Dec 08 '16 at 19:22
  • For $|x|<1$, you have $$ |(-1)^{n} x^{2^{n}}| < |x|^{n}, $$ so the series is majorized by the convergent geometric series $\sum_{n \geq 0} x^{n}$.

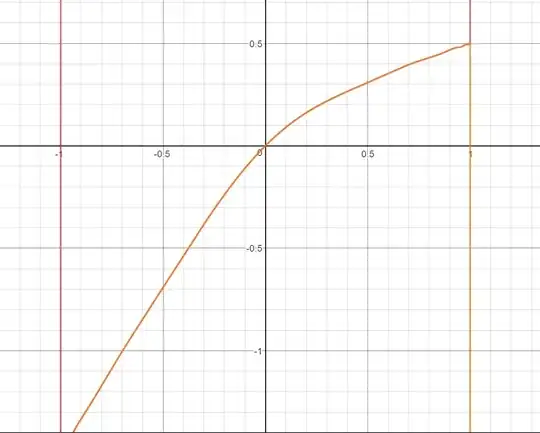
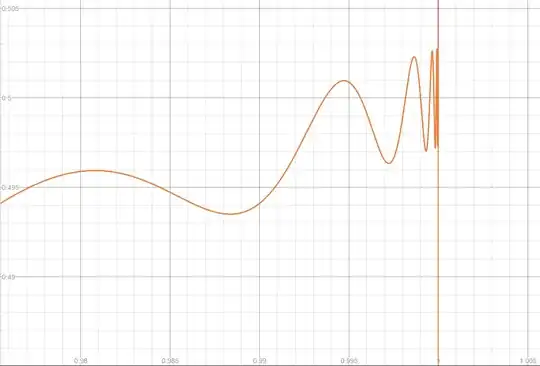
    For $|x| = 1$, the partial sums of the series form the alternating sequence $-1, 1, -1, 1, \ldots, $ hence fail to converge.

     – avs Dec 08 '16 at 19:22
  • @avs But $\lim_{x\to1^-}\sum_{n\ge0}(-1)^nx^n=\frac12$, so I don't see how that helps easily. – Simply Beautiful Art Dec 08 '16 at 19:24
  • @achillehui That's the functional equation I used, and thank you for the link. – Simply Beautiful Art Dec 08 '16 at 19:27

0 Answers0