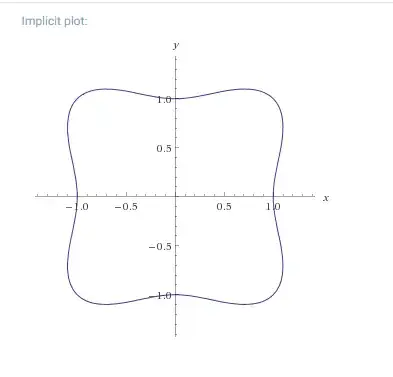
Find the area inside the plot $x^4+y^4=x^2+y^2$.
5 Answers
Using polar coordinates, we have $x = r\cos \theta, y = r\sin \theta\implies x^4+y^4 = r^4(\cos ^4 \theta + \sin^4 \theta)= r^4(1 - 2\sin^2\theta\cos^2\theta)= x^2+y^2 = r^2\implies r^2 = \dfrac{1}{1-2\sin^2\theta\cos^2\theta}\implies r = \dfrac{1}{\sqrt{1-2\sin^2\theta\cos^2\theta}}\implies \text{Area} = 4\displaystyle \int_{0}^{\frac{\pi}{2}}\int_{0}^{\frac{1}{\sqrt{1-2\sin^2\theta\cos^2\theta}}}rdrd\theta$. Can you continue?
- 77,651
Polar form is
$$
r^4\left(\cos^4(\theta)+\sin^4(\theta)\right)=r^2\tag{1}
$$
which gives
$$
r^2=\frac1{\cos^4(\theta)+\sin^4(\theta)}\tag{2}
$$
The area is
$$
\begin{align}
\frac12\int_0^{2\pi}r^2\,\mathrm{d}\theta
&=\frac12\int_0^{2\pi}\frac{\mathrm{d}\theta}{\cos^4(\theta)+\sin^4(\theta)}\tag{3}\\
&=\frac12\int_\gamma\frac{8}{z^4+6+z^{-4}}\frac{\mathrm{d}z}{iz}\tag{4}\\
&=\frac4i\int_\gamma\frac{z^3\,\mathrm{d}z}{z^8+6z^4+1}\tag{5}\\
&=\frac1i\int_\gamma\frac{\mathrm{d}z^4}{z^8+6z^4+1}\tag{6}\\
&=\frac4i\int_\gamma\frac{\mathrm{d}z}{z^2+6z+1}\tag{7}\\
&=8\pi\operatorname*{Res}_{z=-3+2\sqrt2}\left(\frac1{z^2+6z+1}\right)\tag{8}\\[6pt]
&=\sqrt2\,\pi\tag{9}
\end{align}
$$
Explanation:
$(3)$: apply $(2)$
$(4)$: $z=e^{i\theta}$, so $\mathrm{d}\theta=\frac{\mathrm{d}z}{iz}$, $\cos(\theta)=\frac12\left(z+z^{-1}\right)$, $\sin(\theta)=\frac1{2i}\left(z-z^{-1}\right)$
$(5)$: algebra
$(6)$: $\mathrm{d}z^4=4z^3\,\mathrm{d}z$
$(7)$: if $z$ goes around the origin once, $z^4$ goes around $4$ times
$(8)$: use the Residue Theorem
$(9)$: the residue of $\frac1{z^2+6z+1}$ at $z=-3+2\sqrt2$ is $\frac1{2z+6}=\frac1{4\sqrt2}$
- 345,667
Let's look at the area below the part of the curve from $(0, 1)$ to $1, 1)$ and the line $y = x$. The total area is 8 times this.
The area below $y = x$ is obviously $1/2$.
If $x^4+y^4=x^2+y^2 $, $y^4-y^2 =x^2-x^4 $ or, trying to be clever, $y^4-y^2+1/4 =x^2-x^4-1/4+1/2 $ or $(y^2-1/2)^2 =1/2-(x^2-1/2)^2 $ or $y^2 =\frac12+\sqrt{\frac12-(x^2-\frac12)^2} $ so that $y =\sqrt{\frac12+\sqrt{\frac12-(x^2-\frac12)^2}} $.
At the moment, I don't know how to integrate this.
But, Wolfy numerically says that $\int_0^1 y dx \approx 1.05536 $, so the area between this ans $y=x$ is about $0.55536 $ so that the total area is about $8*0.55536 =4.44288 $
- 107,799
After proceeding with the polar coordinate, it suffices to evaluate the following: $$I = 4\int_{0}^{\frac{\pi}{2}}\dfrac{d\theta}{2-\sin^2(2\theta)}= 2\int_0^{\pi}\dfrac{dx}{2-\sin^2x}$$.
Now do a tangent substitution: $$\tan x = t\Rightarrow \sin^2x = \dfrac{t^2}{1+t^2},\,\, dx = \dfrac{dt}{1+t^2}$$
Finally, $$I = 4\int_0^{\infty}\dfrac{dt}{2+t^2} =2\sqrt{2}\cdot(\arctan(\infty) - \arctan(0)) = \sqrt{2}\pi = 4.4429...$$
Or this is also a routine exercise on complex contour integration using the Euler identity $\sin x = \dfrac{e^{ix}-e^{-ix}}{2i}$.
- 13,888
It will be very hard to get the area by analytical integration. I would recommend one stochastic method for attacking the problem. Basically you can use Monte Carlo sampling method to estimate the area. The detailed procedure could be something like this:
Simply you can get the bound of $x$ by solving $y^{'}(x_0)=0$ then you would know $x\in [0,x_0]$ in first quadrant. According to symmetry you know $y\in [0,x_0]$. Then you generate a random number $\eta\in [0,1]$, and take $x= \eta_1 x_0$, $y=\eta _2 x_0$. Denote number of pair $(x,y)$ that is inside the first quadrant as $n$, then you check whether $x$ and $y$ could meet $x^4+y^4-x^2-y^2<=0$, if it meets the equation then you add 1 to $n$ by $n= n+1$. So you do this sampling for a certain number of times, like $N_s$, then the area of first quadrant could be written as
$S= \frac{n}{N_s}x_0^2$.
It is noteworthy that $S$ obtained by this stochastic method is not the true area, but rather a mean which will be approaching the true area if you increasing the sampling times.
- 456
$\int_0^{\pi /2}\frac{1}{(1-2sin^2\theta cos^2\theta)}d\theta$
– duanduan Dec 05 '16 at 06:05