Passing an ellipse through 3 points (where 2 two points lie on the ellipse axes)? [Updated with alternative statement of problem and new picture]

Question

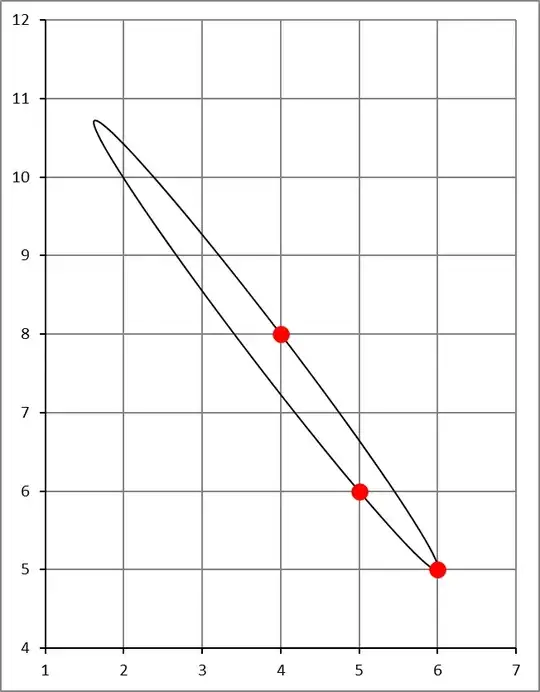
Update

Alternative Statement of Problem, with New Picture

Given three points $P_1$, $P_2$, and $P_3$ in the Cartesian plane, I would like to find the ellipse which passes through all three points, subject to the following constraints:

1. $P_1$ and $P_2$ lie on axes of the ellipse.

2. $\|P_2-P_3\|\le\|P_2-P_1\|$, that is, $P_2$ is not farther from $P_3$ than from $P_1$. (If this is not the case, we can simply swap the labels of $P_1$ with $P_3$ to ensure that it is.)

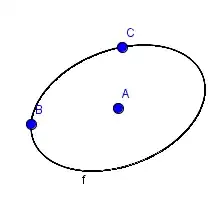
In the picture below, let $O$ be the center of the ellipse and let $F_1$ and $F_2$ be foci. Also let $P_1\prime$ and $P_2\prime$ be the points opposite $P_1$ and $P_2$, respectively, on the ellipse. These points $O$, $F_1$, $F_2$, $P_1\prime$, and $P_2\prime$ are unknowns to solve for. How do I find them? (Note: this is not homework!)

Here’s what I know

1. The center point $O$ lies on a circle passing through diametrically opposed points $P_1$ and $P_2$ (shown as a dotted line in orange) because the angle ${\angle}P_1OP_2$ must be 90°.
2. $\|P_i-F_1\| + \|P_i-F_2\| = 2r$,   $i \in \{1,2,3\}$.    (The sum of the distances from any point on an ellipse to the foci is a constant value, in this case $2r$.)
3. $\|P_2-P_2\prime\| = 2r$    and    $\|P_2-O\|=r$.    (Follows from #2.)
4. $\|P_1-O\|^2 + \|P_2-O\|^2 = \|P_2-P_1\|^2$.   (Pythagorean Theorem applied to ${\triangle}P_1OP_2$. Follows from #1.)

What am I missing?

Intuition tells me there must be some simple way to find $O$, $F_1$, $F_2$, and $r$ — and yet I don’t see where to take it from here.

Below is the original statement of the problem, before the update. The original statement takes more of an algebraic approach, whereas this new statement above takes more of a geometric approach.

---

Original Statement of Problem

How can I find the unique ellipse that passes through three distinct points P₁, P₂, and P₃, such that P₁ and P₂ lie on the axes of the ellipse, and such that P₂ is closer to P₃ than it is to P₁? (P₃ could also lie on the same axis as P₁ in the simplest case, but won’t it ever lie on the same axis as P₂ because the points are distinct.) More specifically, what I want to find is actually the angle θ with which the axis coincident with P₁ is rotated with respect to the x-axis, because this will tell me the angle of the line of tangent at P₂, which is what I’m ultimately interested in.

This is not homework. This is for piecewise (local) curve-fitting of an arbitrary collection of points, where the fitted curve passes through each point using cubic Bézier curve segments. For every triplet of consecutive points, I want to pass an imaginary ellipse through the points, with the middle point (e.g., P₂) provides a pleasing tangent line from which to derive a pair of Bézier control points. This will provide C₁ continuity in the final curve.

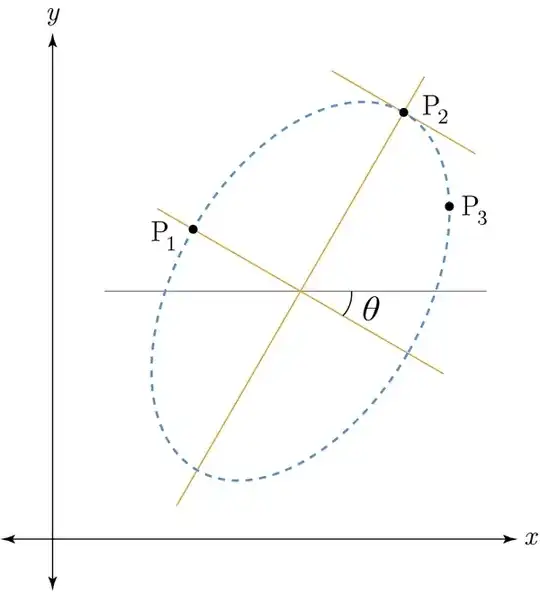
Approaches I have tried so far

1. The first approach I tried was to describe the ellipse parametrically and then scale, rotate, and translate it — and then formulate that as an equation to solve in terms of $\theta$. That ended up reducing to: $$ \Big(\frac{A\cos\theta - B\sin\theta}{C\sin\theta - D\cos\theta}\Big)^2 + \Big(\frac{E\cos\theta + F\sin\theta}{G\sin\theta + H\cos\theta}\Big)^2 = 1 $$ where $A$,$B$,$C$,$D$,$E$,$F$,$G$,$H$ are various vector components of deltas between the three points, but that didn't get me anywhere because I have no idea how to solve that.

2. The second approach I tried was to try to calculate $\theta$ as a function of the ratio of $\|\vec{P_2}-\vec{P_3}\|$ over $\|\vec{P_1}-\vec{P_2}\|$, but I was mistaken that this would lead me anywhere, since in hindsight I believe the ratio is only helpful here for circles rather than ellipses.

3. The third approach I tried was to develop a formula for a general ellipse with center $(u,v)$, semi-major/minor axis lengths $\alpha$ and $\beta$, and rotation $\varphi$. This gave me $$ \Big(\frac{(x-u)\cos\varphi + (y-v)\sin\varphi}{\alpha}\Big)^2 + \Big(\frac{-(x-u)\sin\varphi + (y-v)\cos\varphi}{\beta}\Big)^2 = 1 $$ which is all well and good, but I can’t see where to go with it.

4. The fourth approach I tried was to write the ellipse in general bivariate quadratic form $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 , \quad\textrm{(with A,B,C not all zero)} $$ in which ellipses are represented when $B^2 - 4AC < 0$, and then write out three linear equations of $A$,$B$,$C$,$D$,$E$,$F$ using $P_1$, $P_2$, and $P_3$ as follows: $$Ax_1^2 + Bx_1y_1 + Cy_1^2 + Dx_1 + Ey_1 + F = 0$$ $$Ax_2^2 + Bx_2y_2 + Cy_2^2 + Dx_2 + Ey_2 + F = 0$$ $$Ax_3^2 + Bx_3y_3 + Cy_2^2 + Dx_3 + Ey_3 + F = 0$$ Where I’m stuck right now is how to codify the $B^2 - 4AC < 0$ requirement into this system of linear equations, and how to codify that $P_1$ and $P_2$ lie on the axes of the ellipse.

Other approaches?

I’m out of ideas. I would think the solution is actually probably rather simple, perhaps involving a few inverse sines or cosines and a square root or two. I haven’t been able to find this particular problem stated anywhere (and therefore no conveniently packaged solution), but I’m sure it can’t be all that unusual.

I did have the idea to take my first partial solution (listed above) and do some sort of iterative binary search for $\theta$ (trying different values until the curve passes through $P_3$), but I am much more interested in a closed-formula solution, because this will be executed in a loop over hundreds or thousands of point sets.

Answer 1

Solve for the center $O$ of the ellipse: We know that $O$ is on the circle with $P_1P_2$ as diameter and can verify whether or not $P_3$ is on the corresponding ellipse. We have: $$\tag1\langle P_1-O,P_2-O\rangle=0$$ $$\tag2\frac{\langle P_3-O,P_1-O\rangle^2}{\langle P_1-O,P_1-O\rangle^2}+\frac{\langle P_3-O,P_1-O\rangle^2}{\langle P_2-O,P_2-O\rangle^2}=1$$ I am afraid that equation $(2)$ is of two high a degree to allow unique solutions (I bet there are at least four in the general case).

Why not simply use an approximation, after all you will use the ellipse itself as an approximation only? If $M$ is the middle between $P_1$ and $P_3$, assume that the tangent at $P_2$ should be orthogonal to $MP_2$.

Answer 2

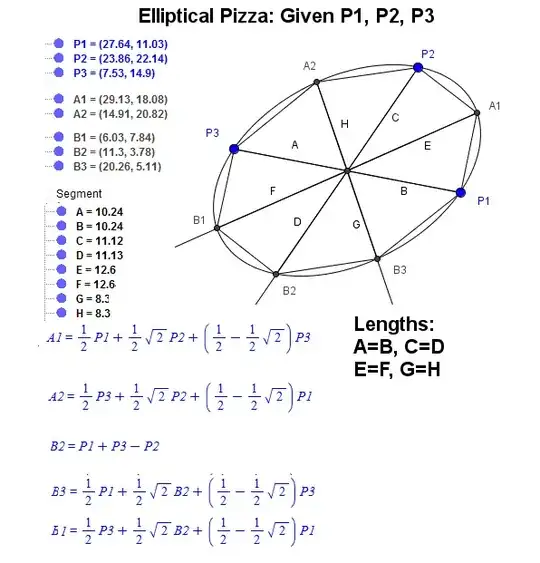I think I found an answer: I called it the ]2 , once you find 2 additional points using the formulas you find the conic through 5 points as here Conic through 5 points. Technically to be exactly like the submitter's drawing you would know what I call A1 and P1 would be unknown but it's the same system of equations ...

I posted it on my blog here: Elliptical Pizza on Ben Paul Thurston Blog

Answer 3

Actually I was suggesting my above answer to the people at geogabra and they told me about this nice parametric equation that only needs the center point and any 2 points on the ellipse, where A is the center: f(t)=A+(B-A)*sin(t)+(C-A)*cos(t)

Answer 4

As the OP remarked, the center of the ellipse must lie on the circle whose diameter is the segment $P_1 P_2 $. Therefore,

Let $M = \dfrac{1}{2} (P_1 + P_2) $ and $u_1 = \dfrac{1}{2}(P_2 - P_1)$ and let $u_2$ have the same length as $u_1$ and be perpendicular to it.

Then the center of the ellipse is given by

$ C = M + u_1 \cos t + u_2 \sin t $

Te parametric equation of the ellipse is given by

$ p(s) = C + (P_1 - C) \cos s + (P_2 - C) \sin s$

The point $ P_3 $ is on this ellipse, therefore,

$\begin{equation} \begin{split} P_3 &= (1 - \cos s - \sin s) C + P_1 \cos s + P_2 \sin s \\ &= (1 - \cos s - \sin s) (M + u_1 \cos t + u_2 \sin t) + P_1 \cos s + P_2 \sin s \end{split} \end{equation}$

Applying the dot product of both sides of the equation with $u_1$ and $u_2$, gives us

$P_3 \cdot u_1 = (1 - \cos s - \sin s) ( M \cdot u_1 + \| u_1 \|^2 \cos t ) + (P_1 \cdot u_1) \cos s + (P_2 \cdot u_1) \sin s $

and

$P_3 \cdot u_2 = (1 - \cos s - \sin s ) (M \cdot u_2 + \|u_2\|^2 \sin t ) + (P_1 \cdot u_2) \cos s + (P_2 \cdot u_2) \sin s$

From the above two equations, it follows that

$ \cos t = \dfrac{1}{\|u_1\|^2} \bigg( - M \cdot u_1 + \dfrac{ P_3 \cdot u_1 - (P_1 \cdot u_1) \cos s - (P_2 \cdot u_1) \sin s }{ 1 - \cos s - \sin s } \bigg)$

$\sin t = \dfrac{1}{\|u_2\|^2} \bigg( - M \cdot u_2 + + \dfrac{ P_3 \cdot u_2 - (P_1 \cdot u_2) \cos s - (P_2 \cdot u_2) \sin s ) }{ 1 - \cos s - \sin s } \bigg)$

which are of the form:

$ \cos t = \dfrac{A_1 \cos s + A_2 \sin s + A_3 }{ 1 - \cos s - \sin s }$

$ \sin t = \dfrac{B_1 \cos s + B_2 \sin s + B_3 }{ 1 - \cos s - \sin s } $

Now apply the identity $\cos^2 t + \sin ^2 t = 1 $, then

$ \bigg(A_1 \cos s + A_2 \sin s + A_3\bigg)^2 + \bigg(B_1 \cos s + B_2 \sin s + B_3\bigg)^2 = (1 - \cos s - \sin s )^2$

Set $ x = \cos s $ and $ y = \sin s $ then $(x, y)$ satisfies two equations, the first of which is

$ x^2 + y^2 = 1 \hspace{30pt}(1)$

and the second is

$ C_1 x^2 + C_2 y^2 + C_3 xy + C_4 x + C_5 y + C_6 = 0 \hspace{30pt}(2) $

where

$ C_1 = A_1^2 + B_1^2 $

$ C_2 = A_2^2 + B_2^2 $

$ C_3 = 2 (A_1 A_2 + B_1 B_2 - 1 )$

$ C_4 = 2 (A_3 A_1 + B_3 B_1 + 1 )$

$C_5 = 2 ( A_3 A_2 + B_3 B_2 + 1 )$

$ C_6 = A_3^2 + B_3^2 - 2 $

Solving the system of $(1)$ and $(2)$ can give upto $4$ solutions for $(x,y)$.

Having obtained $(x,y)$ we can find $\cos t $ and $\sin t $ from the above equations, then the center of the ellipse is determined as well as its axes.

I ran the above method on the following points

$ P_1 = (6,5) , P_2 = (4, 8) , P_3 = (5, 6) $

I obtained $4$ possible ellipses, shown below.

Answer 5

@Rahul, the equation you gave ( $1+xcosϕ+sinϕ(1-x^2+y^2)/(2y)=ycscϕ$ ) can be rewritten in terms of $τ=tan(ϕ/2)$ and the zeros of that expression are given by zeros of the quartic factor, $τ^4y^2 + 2τ^3y(x - 1) + 2τ^2(x^2 - 1) - 2τy(x + 1) + y^2$. Although this permits 4 roots, physically I think you will get 2 real roots and 2 imaginary. The real roots will correspond to the major axis of the ellipse passing through $P_1$ or $P_2$. @Todd-Lehman: the additional constraint you may wish to apply is that the major axis go through your midpoint. In that case, the desired root is chosen to be the the one that gives a line passing through $P_2$ and between $P_1$ and $P_3$.