Show that (using Kripke models) formula $\phi:p\vee (p\to q)$ is not tautology in intuitionistic logic.
My proof*
Above, you can see my trial. Check it please and try to help me defeat my doubts:
1. In each leaf $l$: $l\vdash\not p\leftrightarrow l\vdash \neg p $
Is it true ?
2. In root tree I always can say that: for each variable $p$: $root\not\vdash p, \neg p$
Is it true ?
To prove an intuitionistic tautology, use the intuitionistic inference rules. To show that a sentence is not an intuitionistic tautology, construct a Kripke model. I don't know what you're doing in your attempt, but you should not be attempting to 'prove' anything on a graph. Every non-tautology is witnessed by some Kripke model, but you cannot assume that any graph will do.
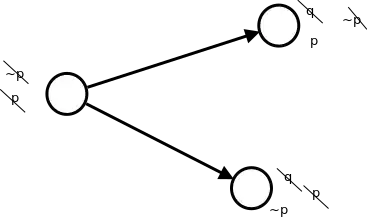
A Kripke model must specify the graph and the values of all the atoms at each node. I first learnt it from Hanno's explanation here, but let me rephrase it in graph terminology. A Kripke model is a directed acyclic graph (its transitive closure is a partial order) where each node is a world such that any atomic sentence that is true in a world is also true in every world reachable from it by a path following the edges in their specified direction (truth is upward-closed in the partial order). Like in classical logic, the sentence "$P \land Q$" is true in a world iff both "$P$" and "$Q$" are true in that world. Likewise the sentence "$P \lor Q$" is true in a world iff either "$P$" or "$Q$" is true in that world. The key difference from boolean algebra is that "$P \to Q$" is true in a world iff "$Q$" is true in every reachable world where "$P$" is true. In other words, "$P \to Q$" is an assertion about the implication in worlds reachable from the current one, and not all worlds as in boolean algebra. Finally "$\neg P$" is defined as "$P \to \bot$". A tautology holds in all worlds in all Kripke models. Do go through the examples Hanno gives to get some idea of how this works, which will also answer your question quite directly.
