1

I am very curious why $\frac{(x-9)}{{\sqrt x}-3}$ and ${\sqrt x}+3$ yields different values (or one is undefined while other gives $6$) at $x=9$ even they are equal. $$ \frac{x-9}{{\sqrt x}-3} = \frac{{({\sqrt x} + 3)({\sqrt x} - 3)}}{{\sqrt x}-3} = {\sqrt x}+3 $$ And some graph plotting websites give the same graph for both functions while google search gives different graphs for the two functions.

N. F. Taussig
  • 76,571
Rusiru Adithya Samarasinghe
  • 61
  • You cannot divide by $\sqrt x -3 $ when it is equal to zero. The first function is undefined for $x=9$. – John Doe Dec 03 '16 at 13:43
  • They're only equal given that $\sqrt{x}-3\neq0$ (which is why you can make the cancellation you have). A function has a domain and codomain as well as a rule, the domain of the first one cannot include $x=9$. – danwalkerdev Dec 03 '16 at 13:43
  • I knew why is it undefined, as I can't divide by zeros. I want to know is why do those give different values even they are equal – Rusiru Adithya Samarasinghe Dec 03 '16 at 13:46

3 Answers3

1

Both functions $\dfrac{x-9}{{\sqrt{x}}-3}$ and ${\sqrt{x}}+3 $ agree over $[0,9)\cup (9,\infty)$, but the first one is not defined at $x=9$ whereas the the latter is.

Olivier Oloa
  • 120,989
  • Does it mean that those two are not equal? – Rusiru Adithya Samarasinghe Dec 03 '16 at 13:47
  • 1
    Stricto sensu those two functions are not equal, the domains are not the same. – Olivier Oloa Dec 03 '16 at 13:48
  • Thanks @Oliver Oloa. Please help me with this also. Then why do we simplify the first one towards next one when we calculate limits. I thought that limits are applied in functions. If they are different how do we say that the seconds one's limit is same of first one – Rusiru Adithya Samarasinghe Dec 03 '16 at 13:52
  • If this was given as a limit as $x\to 9$, then we'd have the determinant value of $\dfrac 00$. We can then to what you've done, to simplify and evaluate. But recall that the limit of $x \to 9, f(x) $ is not to be seen as simply evaluating $f(9)$. – amWhy Dec 03 '16 at 13:57
  • 1
    @user3628865 This is a good question. You may notice that when we write $\lim_{x \to a}f(x)$ this always means $\lim_{x \to a, ,x \neq a}f(x)$. – Olivier Oloa Dec 03 '16 at 13:57
  • @user3628865 You are welcome! – Olivier Oloa Dec 03 '16 at 14:03
0

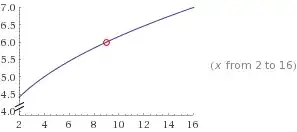
Since division by zero is undefined, your assertion that $$\frac{x - 9}{\sqrt{x} - 3} = \frac{(\sqrt{x} + 3)(\sqrt{x} - 3}{\sqrt{x} - 3} = \sqrt{x} + 3$$ is only true when $x \neq 9$. The function $$f(x) = \sqrt{x} + 3$$ has domain $[0, \infty)$, while the function $$g(x) = \frac{x - 9}{\sqrt{x} - 3}$$ has domain $[0, 9) \cup (9, \infty)$ since division by zero is undefined. Since the functions $f$ and $g$ have different domains, they are not the same even though they agree on the intersection of their domains. The graph of $f$ is continuous, while the graph of $g$ has a hole at the point $(9, 6)$. Therefore, the graphs of $f$ and $g$ are indeed different.

N. F. Taussig
  • 76,571
0

Apparently your question arises in the case of evaluating the limit:

$$\lim_{x\to 9} \frac {x-9}{\sqrt x - 3}.$$ Evaluating the function at $x=9$ yields an indeterminate form $\frac 00$, which does not mean the limit is undefined; what it tells us is that more work needs to be done, in order to understand the behavior of the function as $x$ becomes arbitrarily close to $9$, acknowledging $x \neq 9$.

So we factor out and cancel factors in this case, in order to evaluate the limit as $x\t 9,\;x\neq 9$. T

he cancelation is valid for all $x\neq 9$, so we can do this.

So in this sense, the initial limit is equivalent to $$\lim_{x\to 9} \sqrt x + 3 = 6$$

This is the graph wolfram alpha provides upon entry of $$\lim_{x\to 9} \frac {x-9}{\sqrt x - 3}:$$

enter image description here

amWhy
  • 209,954