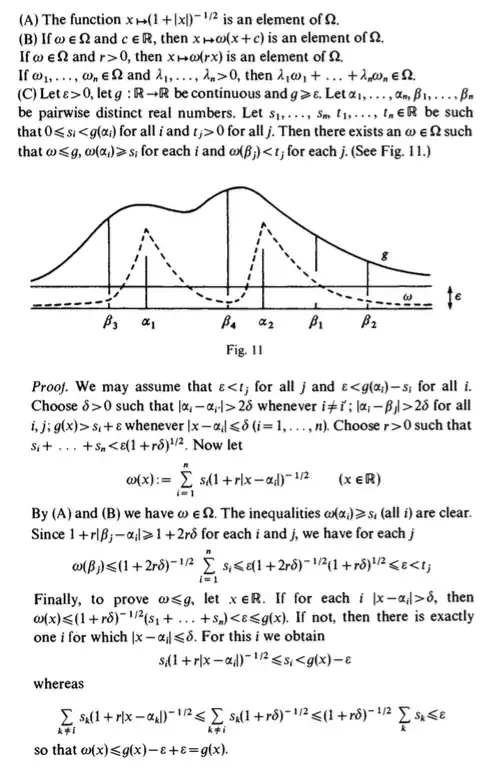
I'm trying to make a problem for my advanced calculus students. I was thinking, if we have a differentiable function $f:\mathbb{R}\to\mathbb{R}$ such that $f'(q)=0$ for all $q\in\mathbb{Q}$, can we say that $f$ is constant?
Asked
Active
Viewed 933 times
9
-
1I do think it is a constant function. – Dec 01 '16 at 15:43
-
1Suppose not, then there is a neighbourhood of some x such that $|f(y)|>a$ for all y in the neighbourhood. – Paul Dec 01 '16 at 15:44
-
4Related: https://en.wikipedia.org/wiki/Pompeiu_derivative – Watson Dec 01 '16 at 16:13
-
(Original article here: https://link.springer.com/article/10.1007%2FBF01449201) – Watson Dec 01 '16 at 16:27
-
6Related: http://math.stackexchange.com/questions/161733/let-f-mathbbr-longrightarrow-mathbbr-a-differentiable-function-such-that – felipeuni Dec 01 '16 at 17:11
-
Derivatives can be very pathological. – Henricus V. Dec 01 '16 at 17:59
-
See also https://en.wikipedia.org/wiki/Minkowski's_question_mark_function#Properties_of_.3F.28x.29 – Watson Jan 16 '17 at 17:46
1 Answers
3
The function $f$ doesn't have to be constant!
A non-constant function $f$ with the required properties is given as Exercise 13.J in A. C. M. van Rooij, W. H. Schikhof, A Second Course on Real Functions, based on an example due to Y. Katznelson and Karl Stromberg, in Everywhere differentiable, nowhere monotone, functions, Amer. Math. Monthly 81 (1974), 349–354, jstor.
Here is a copy of the example:
Another example is has been constructed by Dimitrie Pompeiu in Sur les fonctions dérivées, Math. Ann. 63 (1907), no. 3, 326—332, doi: 10.1007/BF01449201, eudml, GDZ.
You can have a look here.
Martin Sleziak
- 53,687
Watson
- 23,793
-
The wikipedia article states that there are nonconstant differentiable functions whose derivate vanishes on a dense set - how can we guarantee that the rational numbers are contained in this set? – Dominik Dec 01 '16 at 16:42
-
1@Dominik : I agree, this doesn't need to be the case. But the example given in A. C. M. van Rooij, W. H. Schikhof exactly satisfies the condition $f'(x) = 0$ for all rational $x$. – Watson Dec 01 '16 at 16:43
-
Why give this complicated example when the the Pompeiu example, which is proved at the link you gave (thanks), is simpler and is a direct answer to the question of the OP? – zhw. Dec 01 '16 at 21:52
-
@zhw. : AFAIK, in the Pompeiu example, the derivative vanishes on some dense subset (of a closed interval) – as pointed out by Dominik above –, so it doesn't answer completely the OP's request. – Watson Dec 01 '16 at 21:55
-
1No, the wiki. article deals specifically with the rationals in $[0,1].$ (And it doesn't matter; it can be any countable subset of $[0,1].$) Let $f$ be this function. Then $f'(0)=f'(1) =0.$ So we can extend this $f$ to $[0,2]$ as follows: For $x\in [1,2],$ let $f(x) = f(x-1) + f(1)-f(0).$ Now we have a differentiable $f$ strictly increasing on $[0,2]$ such that $f'(q)=0$ for each rational $q\in [0,2].$ We can continue this to the right or left to obtain a strictly increasing differentiable function on $\mathbb R$ whose derivative equals $0$ at each rational $q\in \mathbb R.$ – zhw. Dec 01 '16 at 22:49
-
1@zhw: But the construction from the wikipedia article yields a function whose derivative vanishes in the points $g(p_i)$, where $p_i$ are the rationals in $[0, 1]$. It is not clear why the derivative should also vanish in the $p_i$. – Dominik Dec 02 '16 at 13:08
-
@Dominik Ah, I see. I glossed over that, my bad. Thanks to you and Watson for the correction. – zhw. Dec 02 '16 at 17:09