4

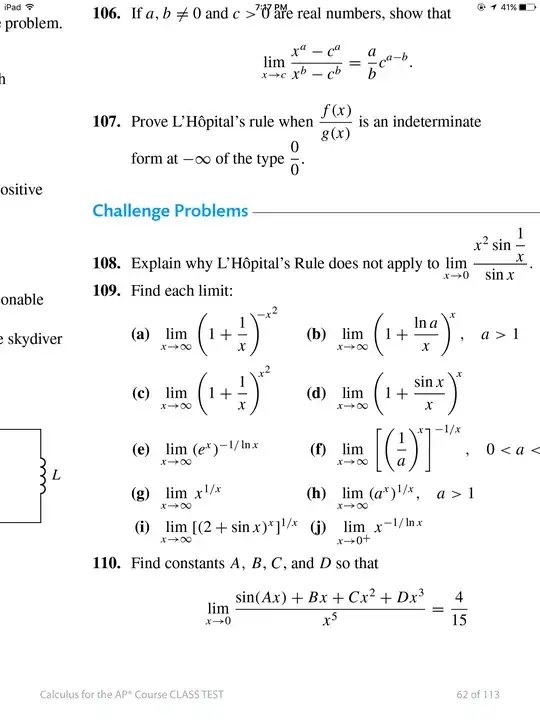
Apparently, Rogawski's Calculus for AP contains the following problem:

108. Explain why L'Hôpital's rule does not apply to

$$ \lim_{x\rightarrow 0}\frac{x^2\sin\frac{1}{x}}{\sin x} $$

It seems to me that it does apply:

The L'Hôpital's rule says: if $\lim_{x\rightarrow c}f(x)=\lim_{x\rightarrow c}g(x)=0$ and both $f$ and $g$ are differentiable at $x=c$ and $g'(c)\ne 0$, then $\lim_{x\rightarrow c}\frac{f(x)}{g(x)}$ exists and is equal to $\frac{f'(c)}{g'(c)}$. (Note that nothing is assumed about differentiability of $f$ and $g$ other than at $x=c$).

  1. Define the numerator $f(x)=x^2\sin\frac{1}{x}$ to be $f(0)=0$ at $x=0$. Now, both numerator $f$ and denominator $g(x)=\sin(x)$ are continuous at $x=0$ and their values are $f(0)=g(0)=0$.

  2. The numerator $f$ is differentiable at $x=0$ and the derivative is $f'(0)=0$ (the derivative itself is discontinuous at 0, but that is irrelevant - even the existence of the derivative at any point other than 0 does NOT matter). One can see that from the definition of the derivative: $f'(0)=\lim_{h\rightarrow 0} \frac{h^2\sin\frac{1}{h}}{h} = \lim_{x\rightarrow 0} h\sin\frac{1}{h} = 0$ (see PS step 2 below).

  3. The denominator $g$ is differentiable at $x=0$ and the derivative is $g'(0)=\cos 0=1$.

  4. Thus the limit is $\frac{0}{1} = 0$.

What am I missing?

PS. Note that I am not asking why the limit is 0. That can be easily seen without L'Hôpital:

  1. $\lim_{x\rightarrow 0}\frac{x}{\sin x} = 1$: this is the inverse of the standard limit $\lim_{x\rightarrow 0}\frac{\sin x}{x} = 1$.

  2. $\lim_{x\rightarrow 0} x \sin\frac{1}{x} = 0$ because $\sin\frac{1}{x}$ is bounded and $\lim_{x\rightarrow 0} x = 0$, this follows from Squeeze theorem.

  3. the Product Rule for Limits implies that $$\lim_{x\rightarrow 0}\frac{x^2\sin\frac{1}{x}}{\sin x} = \lim_{x\rightarrow 0}x\sin\frac{1}{x} \times \lim_{x\rightarrow 0}\frac{x}{\sin x} = 0 \times 1 = 0$$

PPS Here is the scan from the textbook:

enter image description here

sds
  • 4,533
  • It does not apply because of the term $\sin(1/x)$. – Enrico M. Nov 28 '16 at 19:44
  • @AlanTuring: why does a "term" prevent a theorem from being applicable? :-) I mean, this is more or less what my daughter's teacher said, but this makes no sense. IOW, what step in my logic is wrong? – sds Nov 28 '16 at 19:47
  • http://math.stackexchange.com/questions/534090/the-limit-of-sin1-x-as-x-to-0-does-not-exists – Enrico M. Nov 28 '16 at 19:48
  • 2
    Note that L'Hospital's rule says that $\lim\limits_{x\to 0} \frac{f(x)}{g(x)} = \lim\limits_{x\to 0} \frac{f'(x)}{g'(x)}$ if a) $f(x) = g(x) = 0$ and b) the limit of the quotients of the derivatives exists. b) isn't fulfilled here. – Daniel Fischer Nov 28 '16 at 19:48
  • You need different approach – Enrico M. Nov 28 '16 at 19:48
  • 1
    Nope. Since $f'$ isn't continuous at $0$, the existence of $\frac{f'(0)}{g'(0)}$ doesn't imply the existence of the limit. – Daniel Fischer Nov 28 '16 at 19:50
  • The special case you linked to says "in the case where $f$ and $g$ are continuously differentiable at the point $c$ and where a finite limit is found after the first round of differentiation", but here $f$ is not continuously differentiable at $0$. – Daniel Fischer Nov 28 '16 at 20:04
  • @DanielFischer: the proof does not use even existence of the derivatives other than at $0$, let along the continuous differentiability assumed. – sds Nov 28 '16 at 20:06
  • @LutzL: the existence of the limit is irrelevant. – sds Nov 28 '16 at 20:09
  • Well, what you wrote that L'Hospital's rule says is true, but it's not what L'Hospital's rule is usually considered to be. Look at the statement on the wikipedia page, that looks quite different. Your rule is much simpler. – Daniel Fischer Nov 28 '16 at 20:09
  • @DanielFischer: alas, you are right about wiki - how would you call the statement I think is called l'Hospital's rule? – sds Nov 28 '16 at 20:13
  • I'd call it an application of Taylor approximation of order $1$. – Daniel Fischer Nov 28 '16 at 20:14
  • As a compromise: As the short proof in wikipedia shows, it is indeed sufficient that $\frac{f'(0)}{g'(0)}$ exists in all components. What the task is after is the use of the theorem as given in the book, so one would need its statement from there, that presumably relies on the existence of the limit of the quotient of derivatives. @sds: Is the quote of the theorem from the book? – Lutz Lehmann Nov 28 '16 at 20:24
  • @sds This link might be useful: http://math.stackexchange.com/questions/1710786/why-does-lhopitals-rule-fail-in-this-case/1710798#1710798 – imranfat Nov 29 '16 at 00:38
  • @LutzL: the quote is from my memory. the book formulates the rule in Daniel Fisher's form, so, I guess, there is no question anymore. Thanks to all of you. – sds Nov 29 '16 at 00:53
  • Someone posted an answer and then deleted it, and I think it was right - that the textbook used the other form of l'H rule. If you could undelete it, I would accept that answer. – sds Nov 29 '16 at 01:01

3 Answers3

4

You have misstated L'Hopital's Rule. It does not say $\lim_{x\to c}{f(x)\over g(x)}={f'(c)\over g'(c)}$ (with the usual assumptions on $\lim_{x\to c}f(x)$ and $\lim_{x\to c}g(x)$). It says

$$lim_{x\to c}{f(x)\over g(x)}=\lim_{x\to c}{f'(x)\over g'(x)}$$

provided the latter limit exists. In this case

$${f'(x)\over g'(x)}={2x\sin(1/x)-\cos(1/x)\over\cos x}$$

for $x\not=0$. So even though $f'(0)=\lim_{x\to0}{f(x)-f(0)\over x}=\lim_{x\to0}x\sin(1/x)=0$ (assuming we let $f(0)=\lim_{x\to0}f(x)=0$), the hypotheses of L'Hopital's Rule are not fulfilled because $\lim_{x\to0}(f'(x)/g'(x))$ does not exist. In particular $\cos(1/x)$ has no limit as $x\to0$.

Barry Cipra
  • 79,832
  • 1
    The problem doesn't even state that $f(0)=0$ though, I think that as written, you can just say $f$ is not defined and therefore notdifferentiable at $0$, and you're done. – Ovi Nov 29 '16 at 01:05
  • Started to write the same thing, but saw you came to the exact point about the existence. – A.Γ. Nov 29 '16 at 01:07
  • @Ovi The function is differentiable after being defined $f(0)=0$, so it is not a problem. The very problem is that the limit of $f'/g'$ does not exist. – A.Γ. Nov 29 '16 at 01:09
  • 1
    @A.G. I completely agree, but I don't see any indication in the problem that they expect us to assume $f(0) = 0$. It just says $\lim_{x \to 0} \dfrac {x^2 \sin \dfrac 1x}{\sin x}$ – Ovi Nov 29 '16 at 01:11
  • @Ovi The function $x^2\sin(1/x)$ is the very known example of being differentiable at the origin. It is about the same as to have $f(x)=x^2$, $x\ne 0$. There is no question how to define it at $x=0$. – A.Γ. Nov 29 '16 at 01:17
  • But $f(x) = x^2\sin (1/x)$ isn't differentiable at $x=0$ because it isn't defined at $x=0$. The function $h(x) = \begin{cases} x^2\sin(1/x), & x\ne0\ 0, & x=0\end{cases}$ is differentiable at $x=0$ but it's a different function. I don't think it's valid to just provide the given function with a specified value at a point outside of its domain, even if it's the "obvious" choice, and especially for something that appears to be at a Calculus I level. –  Nov 29 '16 at 12:25
1

The proof of l'Hopital that the book uses is probably based on the extended mean value theorem, $$ \frac{f(x)-f(c)}{g(x)-g(c)}=\frac{f'(\tilde x)}{g'(\tilde x)} $$ for some $\tilde x$ between $c$ and $x$. This way of replacing the limit with a limit allows to apply the theorem repeatedly. It ignores that one can also reformulate it as a quotient of difference quotients, $$ \lim_{x\to c}\frac{f(x)-f(c)}{g(x)-g(c)}=\frac{\lim_{x\to c}\frac{f(x)-f(c)}{x-c}}{\lim_{x\to c}\frac{g(x)-g(c)}{x-c}}=\frac{f'(c)}{g'(c)} $$ which exists if both functions are differentiable at $x=c$ and $g'(c)\ne0$.

Now when the derivatives are not continuous, one can not conclude about the limit as the book expects. Thus the explored situation is not covered by the assumptions of the used theorem.

In general I find it often more instructive to use the mean value theorem (or Taylor expansion) than l'Hopital.

Lutz Lehmann
  • 126,666
  • l'Hopital does NOT require the existence of the derivatives in the neighborhood - just at the limit point. – sds Nov 28 '16 at 19:50
  • Please explain the recent down-voting after I edited to conform to the results of the discussion in the comments to the question. – Lutz Lehmann Nov 29 '16 at 10:31
  • 1
    I replaced my old downvote with an upvote. – sds Nov 29 '16 at 13:42
  • @sds L'Hopital's rule does require that f'/g' to be definen on a set S=J{a}, where J is an open interval containing a. Otherwise the limit makes no sense. Limits do not exist at isolated points. – Ovi Nov 29 '16 at 17:22
  • @Ovi: we rehashed this yesterday. – sds Nov 29 '16 at 17:31
0

The problem is your $f(x) = x^2 \sin \dfrac 1x$ is not differentiable at $0$, because $f$ is not even defined at $0$. A definition of the derivative is $\lim_{x \to a} \dfrac {f(x) - f(a)}{x-a}$, so as you can see it is required that $f$ be defined at $a$.

Ovi
  • 23,737
  • 2
    no, $f$ is differentiable everywhere (although the derivative is discontinuous at 0). Moreover, this is the canonical example of such a function. – sds Nov 29 '16 at 00:54
  • 1
    @sds Not the way you wrote it. If you define $f(0)$ as $0$ then yes, it is differentiable at $0$. But just $x^2 \sin \dfrac 1x$ is not defined at $0$ so it can't be differentiable there. – Ovi Nov 29 '16 at 01:02
  • What Ovi said. It's not ok to just give functions values at points outside their domains, even if those values are the "obvious" choices. Then they just become different functions.. –  Nov 29 '16 at 12:34