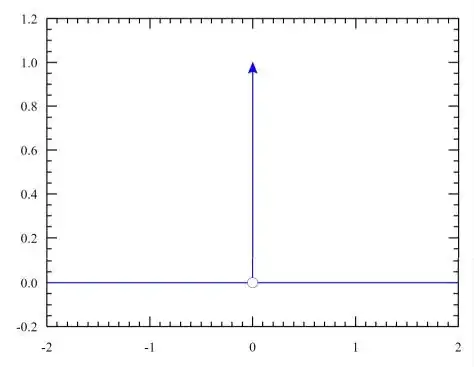
The term you're looking for is distribution theory. In the language of distributions, it is extremely simple to make the Dirac delta "function" rigorous, and to prove the aforementioned properties.
Here's the basic notion of a distribution:
A distribution is a continuous linear map from a set of nice functions (called "test functions") to $\mathbb{R}$.
Notice, by the way, that this means distributions are actually honest-to-satan functions. However, they're functions that eat other functions, which makes them somewhat different from, say, functions on the real line. For one thing, it's probably not immediately clear how to define a "derivative" or anything else. Once we look at the details, we'll find a way around this pretty quickly.
When we pick different sets of test functions, we get different notions of "distribution." To begin with, let's choose our space of test functions $D$ be the set of infinitely differentiable functions $\mathbb{R}^d \to \mathbb{R}$ that have compact support (that is, we require the functions to be zero except on some compact set). We need some topology on $D$ in order to make sense of the term "continuous." (If you're not familiar with topologies and convergence, skip the next line for now.) The topology on $D$ is usually given by specifying what convergence means on $D$: we will say that a sequence of elements $\varphi_k$ in $D$ converges to $\varphi$ as $k \to \infty$ if and only if every derivative of $\varphi_k$ converges uniformly to the corresponding derivative of $\varphi$ and all the $\varphi_k$ have supports contained in a common compact set.
An example of a distribution is the map $D \to \mathbb{R}$ given by
$$\varphi \mapsto \varphi(0)$$
You can check that this is a continuous linear map. This map is the Dirac delta "function" $\delta$.
Another example: Say we have a locally integrable function $f: \mathbb{R}^d \to \mathbb{R}$. Then we can define another distribution
$$\varphi \mapsto \int f(x) \varphi(x) dx$$
Now this is linear in $\phi$, and is continuous. I'll write $(f, \varphi)$ for this distribution.
Perhaps somewhat confusingly, when $F$ is a distribution (not a locally integrable function like $f$) we often use the conflicting notation $(F, \varphi)$ to indicate some distribution applied to $\varphi$.
Keep in mind that the first example above cannot be written in the form of the second example, i.e. as integration against a locally-integrable function, but is nonetheless the notation that is often used, particularly in physics: $\int \delta(x) f(x) dx = f(0)$. This is a pretty common sleight of hand: we pretend that distributions are given by integrating against a nice function even though not all distributions can be written this way.
Now we want to define a notion of "derivative" for distributions. Since a distribution is a function from a space of functions to the real numbers, it's not immediately clear how to do this. Let's try that aforementioned sleight-of-hand: consider the distributions of the form $\varphi \mapsto \int f(x) \phi(x) dx$ for some locally-integrable $f$.
From the usual integration by parts formula from ordinary calculus,
$$\int \partial_x^{\alpha} f(x) \varphi(x) dx = - \int f(x) \partial_x^{\alpha} \varphi(x) dx$$
(Note that the usual boundary terms in the integration-by-parts formula go away because $\varphi$ has compact support.)
To put this back into the notation from above: $(\partial_x^{\alpha} f(x), \varphi) = - (f(x), \partial_x^{\alpha} \varphi)$. So this suggests a way to define "differentiation:" let's use this notation as a definition.
That is, for any distribution $F\colon D \to \mathbb{R}$, we define the distributional derivative $\partial_x^{\alpha} F$ by $$(\partial_x^{\alpha} F, \varphi): = -(F, \partial_x^{\alpha} \varphi)$$
For example, let's consider the distribution given by (integrating against) the Heaviside function (we're taking $\mathbb{R}^d$ in the definition of $D$ to be $\mathbb{R}^1$):
$$
H(x) =
\begin{cases}
1 &(x >0)\\
0 &(x\leq 0)
\end{cases}
$$
Like in the second example, the distribution defined by $H$ is $(H, \varphi) = \int H(x) \varphi(x) dx$. As an exercise compute the derivative of this from the definition (the answer is at the bottom).
So to recap: A distribution is a continuous linear map from a set of nice functions (called "test functions") to $\mathbb{R}$. A dirty trick we will use again and again in distribution theory is to systematically confuse a function $f$ and the distribution given by integrating against it. Using this trick, we can use relatively basic mathematics to understand what certain notions like integration ought to mean for distributions, and then take this to be the definition. I've shown how to do this with (partial) derivatives; you can do the same with convolutions, adjoints, and more.
The above is just meant to give you a small flavor of the subject, so I won't go any further, and most good analysis texts should have more details if you seek them. A readable source (though not one I personally favor) is Stein and Shakarchi's Functional Analysis, Chapter 3.
Answer:
The distributional derivative of this is:
$$(H', \varphi) = - (H, \varphi') = -\int H(x) \varphi'(x) dx = - \int_{0}^\infty \varphi'(x) dx = \varphi(0) - \lim_{\alpha \to \infty} \varphi(\alpha) = \varphi(0)$$
Notice that the Dirac delta "function" (distribution) applied to $\varphi$ gives precisely the same thing! (Hence the common confusing claim in intro physics classes: "the Dirac delta is just the derivative of the Heaviside function.")