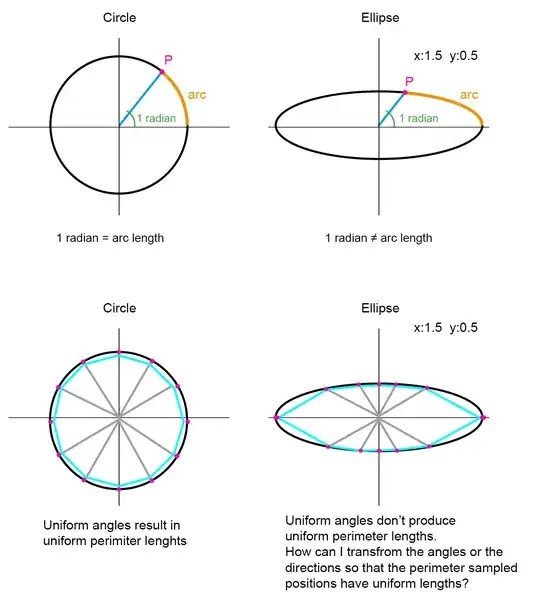
I'm trying to come up with a way that as I progress linearly from $0$ to $360$ degrees or $0$ to $2\pi$ radians I have the the corresponding position (P) on the perimeter of an ellipse to also travel on it at a linear speed movement.
Thanks

I'm trying to come up with a way that as I progress linearly from $0$ to $360$ degrees or $0$ to $2\pi$ radians I have the the corresponding position (P) on the perimeter of an ellipse to also travel on it at a linear speed movement.
Thanks
Suppose the ellipse is parameterized by $x = a\cos\theta$, $y = b\sin\theta$ for $\theta\in[0,2\pi)$. Without restricting generality assume that $b$ is the length of the semi-major axis, i.e., $b > a$. Then the arc length of the portion of the ellipse corresponding to $\theta\in [0,\alpha]$ is given by
$$ bE(\alpha,k) =b\int_0^\alpha \sqrt{1 - k^2\sin^2\theta}\,d\theta, $$
where $k = \sqrt{1 - (a/b)^2}$ and $E(\alpha,k)$ is the incomplete elliptic integral of the second kind. Let $A = bE(2\pi,k)$ be the circumference of the ellipse. If I understand your question properly, then given a sequence of equally spaced points $t_i = Ai/N$ for $i = 0,\ldots,N-1$ you want the corresponding values of $\theta_i$ such that $$ bE(\theta_i,k) = t_i,\quad i = 0,\ldots,N-1. $$ This can be accomplished by numerically inverting the function $E$ for each $t_i/b$ with the restriction that $\theta_i\in[0,2\pi)$. Note that since $E(\alpha,k)$ is strictly increasing, it has an inverse on $[0,\infty)$. If you are interested, I can provide some Octave (Matlab) code to compute the values of $\theta_i$.