2

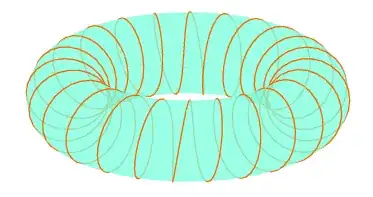
Prove that the following map is smooth and analyse its image as the real number $\alpha$ varies (how does it look like? Is it a submanifold?)

\begin{align*} f_{\alpha}:\mathbb{R}&\to\mathbb{S}^1\times\mathbb{S}^1\\ t&\mapsto (e^{2\pi it}, e^{2\pi \alpha it}) \end{align*}

I've managed to prove that $f_{\alpha}$ is smooth and that $\text{Im}(f_{\alpha})$ is a closed curve on the torus $\Leftrightarrow \alpha\in\mathbb{Q}$. But I'm having trouble to formalize whether or not it is a submanifold of the torus. I actually don't know if it is true when the image is not a closed curve. How can I solve this?

rmdmc89
  • 9,939
  • 2
    What's your definition of a submanifold? Do you require it to be a closed subspace? – Dan Rust Nov 22 '16 at 16:51
  • I'm considering a submanifold as just a subset of the torus which is also a manifold itself. Intuitively, I belive the closed curve is a submanifold, but otherwise, I can barely visualize the picture, so it's hard to have a hunch – rmdmc89 Nov 22 '16 at 18:46

2 Answers2

3

Should it be $f_{\alpha}(t)=(e^{2\pi i t}, e^{2\pi \alpha i t})$ ?

If so, sure it is a manifold when $\alpha\in\mathbb Q$ (with the proper identification it is simply a curve on $\mathbb R^2$. In this case, it is a curve that spirals around the torus until it closes, much like in the figure:

enter image description here

When $\alpha\not\in\mathbb Q$ the curve is dense in the torus.

Since rational numbers and irrational numbers are dense, it is difficult to say much more about what happens when $\alpha$ varies.

John B
  • 16,854
  • Yes, sorry about the exponents, just corrected it. About the density when $\alpha\notin\mathbb{Q}$, that's what got me unsettled. It just sounds weird to talk about a 1-submanifold which is dense in a 2-manifold. Very conter intuitive to me – rmdmc89 Nov 23 '16 at 11:54
  • You are right, but that's why it is only a manifold when $\alpha\in\mathbb Q$. – John B Nov 23 '16 at 16:43
  • Thanks! Good to know that my intuition was right! But how would I actually prove it isn't a manifold? Any hint would be great! Thanks! – rmdmc89 Nov 23 '16 at 17:52
  • Locally your manifold should be like a line segment. How could that be if it is dense? Any neighborhood will have much more than just a segment and that's all you need to say. – John B Nov 23 '16 at 19:03
  • @Jonas Btw, where did you get this nice illustration? – Evgeny Nov 24 '16 at 21:42
  • Somewhere from the web, entering "geodesics" and "torus". I am not able to do it with Mathematica... – John B Nov 24 '16 at 23:25
  • Source found: http://tex.stackexchange.com/questions/70090/3d-helix-torus-with-hidden-lines – John B Nov 24 '16 at 23:35
2

Let $\alpha \in \mathbb{R}$ be irrational then we know the set $\{m+n\alpha|m,n \in \mathbb{Z} \}$ is dense in $ \mathbb{R}$. Let $x,y \in \mathbb{R}$ and for given $\delta >0 $ there exists $m,n\in \mathbb{Z}$ such that $|x \alpha-y+m+n\alpha|< \delta$. We have $||(e^{2 \pi ix},e^{2 \pi iy})-(e^{2 \pi i(x+n)},e^{2\pi i(x+n)\alpha} )||$=$|1-e^{2 \pi i(x \alpha-y +m+\alpha n)}| $. Since exponential function is continuous at zero for given any $\epsilon >0$ we can bound the quantity with that. Hence, it is dense.

Varadharajan R
  • 323
  • You have posted the same answer to two different questions. When you do this, it creates noise on the website. If you believe that two questions have the same answer, then you should flag one as a duplicate of the other, and only post one answer. – Xander Henderson Nov 19 '20 at 11:51