3

Setting. Suppose we have a scene and a spotlight above it that can be turned onto any object on the scene. On the scene we have an object that moves uniformly and linearly. We are given the angular velocity of the spotlight, the speed of the object and initial positions of both. The question is what is the minimal amount of time before we can put the object in the center of the light spot, and at what angle the spotlight should be moved?

enter image description here

Mathmatical formulation.

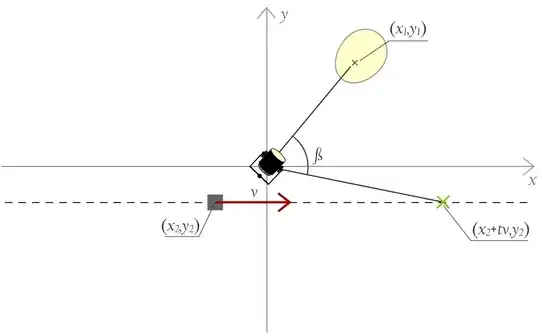
Given. Let consider 3d space with Cartesian coordinate system so that the object moves on the plane $xOy$ parallel to the $x$-axis, spotlight is hang at the point $(0,0,h)$ and shines onto $(x_1,y_1,0)$, i.e. onto $(x_1,y_1)$ on the plane $xOy$. The spotlight angular velocity is $\varphi$. The object initially starts at the point $(x_2,y_2)$ and moves at the speed $v$, so the velocity vector is $(v, 0)$ (or globally $(v, 0, 0)$).

To find. The minimal amount of time $t$ before we can put the object in the center of the light spot is the unknown. By that time the object will reach the position $(x_2+t\cdot v, y_2)$, so the spotlight would have to move directly from $(x_1,y_1)$ onto $(x_2+t\cdot v, y_2)$ by turning through an angle $\beta$, which is the angle between vectors $(x_1,y_1,-h)$ and $(x_2+t\cdot v, y_2, -h)$.

Equation. The above gives us the following equation: $$ \frac{\beta}{\varphi} = t, $$ where $\beta$, as was defined before, is the angle between vectors $(x_1,y_1,-h)$ and $(x_2+t\cdot v, y_2,-h)$. Using the formula for cosine between two vectors — $\cos{\beta}=\frac{\overline{a}\cdot \overline{b}}{|\overline{a}|\cdot|\overline{b}|}$ — we get:

$$ \frac{1}{\varphi}\cos^{-1}\frac{x_1(x_2+t\cdot v)+y_1\cdot y_2 + h^2}{\sqrt{\left(x_1^2+y_1^2+h^2\right)\left((x_2+tv)^2+y_2^2+h^2\right)}} = t, $$

This is too hardcore to my taste and I have no idea how to solve it. Of course I could use the fixed-point iteration to approximate $t$, but I was hoping for the exact solution. Besides I could also run an iterative procedure before formulating this formula, by moving the spotlight onto the current object position, see where the object occures after this and next time move the spotlight onto that new position, and so on. But again this would only approximate the desired result. Is there a way to solve this monstrous equation? Maybe we can reformulate the problem so the equation simplifies? Thank you very much in advance!

Glinka
  • 3,182

1 Answers1

1

This is not a complete proof that no closed-form solution exists, but it is suggestive.

Your equation can be written as $$\frac1\phi\cos^{-1}\frac{p(t)}{\sqrt{q(t)}}=t,$$ where $p(t)$ and $q(t)$ are linear and quadratic polynomials in $t$ respectively. As $\cos^{-1}$ maps $[-1,1]$ to $[0,\pi]$ and it is bijective in that interval, this is equivalent to finding the roots of $$p(t)=\sqrt{q(t)}\cos(\phi t)$$ in the interval $t\in[0,\pi/\phi]$.

If we take $p(t)=t$, $q(t)=1$, and $\phi=1$, we obtain $$t=\cos t,$$ for which no closed form seems to be known. That said, while it is easy to choose parameters of the original problem so that $p(t)=t$ and $\phi=1$, we cannot actually obtain $q(t)=1$, so $t=\cos t$ is not a special case of the original problem.

The point is only that the problem is extremely similar to a much simpler one that itself has not been solved in closed form.

Community
  • 1