Solve equation based on modulus function.

Question

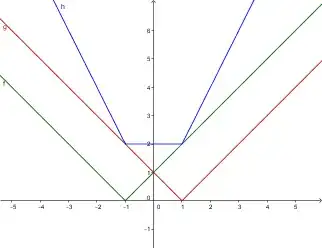
Question:

Explain algebraically how to solve for x in this equation:

$$|x+1| + |x-1| = 2$$

Where the result should be $ -1 \le x \le 1 $.

Also, why is it that an inequality originates from this equation ?

Context:

So far I have seen that $|x| = |a| \Leftarrow \Rightarrow x^2 = a^2$, but when I apply this rule I get $x = 0$, which in itself is true, but does not give the correct answer.

Based on the definition of absolute values, one can deduce that $x$ is either $-1$ or $1$. But I just don't understand where the inequality comes from.

Answer 1

Have a look at this sketch:

We have the graphs of $\lvert x+ 1\rvert$ (green), $\lvert x - 1\rvert$ (red) and the sum of both (blue). We are interested where the sum has the value $2$. This is the interval $[-1,1]$.

Answer 2

Hint: Take different cases where $x$ belongs to one of this intervals:

$$(-\infty-1],\;[-1,1],\;[1,+\infty)$$