How would you prove that $f_n(x) = x^{1/n}$ converges pointwise to $1$ for $x \in (0, \infty)$? It's obvious if you take the limit as $n \to \infty$ but how would you prove it using epsilon?
Asked
Active
Viewed 141 times
2
-
1On which domain? $f_n(0)=0$ for all $n$. – lhf Nov 17 '16 at 16:39
-
Let's say for $x \in (0, \infty)$. – mil10 Nov 17 '16 at 16:40
-
Pointwise or uniformly? – rlartiga Nov 17 '16 at 16:42
-
@rlartiga pointwise. – mil10 Nov 17 '16 at 16:43
-
First prove that the sequence $(\sqrt[n]{n})$ is bounded and monotone, and then convergent. Then you will know that any sequence of the kind $(\sqrt[n]{x})$ for $x\in\Bbb R_{>0}$ converges to $1$. Here some hints. – Masacroso Nov 17 '16 at 17:00
-
Is the sequence uniformly convergent on $X=(0,1)$? – Ramen Sep 18 '17 at 16:52
3 Answers
1
If $x^{1/n} \to 1$ pointwise then:
For all $\varepsilon > 0$, there exist an $N_x > 0$ such that $|x^{1/n}-1|<\varepsilon$ for all $n > N_x$.
Let's split this in to two cases: $x > 1$ and $0 < x < 1$.
If $x>1$ then $x^{1/n} > 1$ for all $n \in \mathbb N$, and hence $x^{1/n}-1>0$.
If $x^{1/n}-1>0$ then: $|x^{1/n}-1|<\varepsilon \iff x^{1/n}-1<\varepsilon$.
Let's try to find an $N$ for which $x^{1/n}-1<\varepsilon$, for all $n > N$.
If $x^{1/n}-1 < \varepsilon$ then $x^{1/n} < \varepsilon+1$. We can log both sides, and since log is an increasing function, it preserves the direction of the inequality.
\begin{eqnarray*} \log(x^{1/n}) &<& \log(\varepsilon+1) \\ \\ \frac{1}{n}\log x &<& \log(\varepsilon+1) \\ \\ \frac{1}{n} &<& \frac{\log(\varepsilon+1)}{\log x} \\ \\ n &>& \frac{\log x}{\log(\varepsilon+1)} \end{eqnarray*}
Notice dividing by $\log x$ didn't change the direction of the inequality because $x>1$ and $\log x > 0$.
Can you do the same for $0<x<1$?
Fly by Night
- 32,272
0
$\lim_{n\rightarrow\infty} x^{1/n}=x^{\lim_{n\rightarrow\infty} 1/n}= x^0 = 1$ for any $x>0$ (by continuity of the exponential function).
mathematician
- 2,450
-
How do we know this is true? I'm not sure we learned this property of limits yet. I also know that if you take $n \to \infty$ then the proof is obvious, but I have to solve it using epsilon. – mil10 Nov 17 '16 at 16:56
-
By the definition of continuity (in terms of limits) and the fact that $b^x$ is continuous (where we're using the letter $x$ for our base in this question/answer). – mathematician Nov 17 '16 at 16:57
-
To prove using epsilons and deltas, this is the same as proving the function $f(x)=b^x$ is continuous at zero. You would take $\delta = \log_b(\epsilon)$ I think. – mathematician Nov 17 '16 at 16:59
-1
The user @mathematician already gave a proof using limit's properties, let us now prove it by the epsilon-delta definition of limit.
I will start by writing it for the particular case when $x \to \infty $:
$$\lim_{x \to \infty} f(x) = L \iff \forall_{ \epsilon > 0}\ \exists_{\delta > 0}: x > \frac{1}{\delta } \Rightarrow |f(x) - L| < \epsilon $$
Let us fix some $\epsilon > 0$. We want to show that $f(x) \to 1$ as $x \to \infty $.
The condition for the existance of $\delta $ is equivalent to finding a lower bound $b $ such that $x > b \Rightarrow |f(x) - 1| < \epsilon $.
Pausing for a moment we realize that for $x > 1, \sqrt[x]{x} > 1$ thus if $f(x) $ is to fall under a distance shorter than $\epsilon $ of 1, we must have $f(x) < 1 + \epsilon $.
Now we just rewrite our inequality:
$$\sqrt[x]{x} < 1 + \epsilon \iff x < (1 + \epsilon)^x $$
This is trivially satisfied by $x = 1$, for any $\epsilon $, but surely $b \not = 1$ for any $\epsilon $. For example, taking $\epsilon = 0.01$, surely we don't have $2 < (1 + 0.01)^2$.
What one sees is that the inequality $x < (1 + \epsilon)^x $ is satisfiable for very small $x $, and then for very big values of $x $. This means your lower bound $b $ is the value of $x $ for which any value above satisfies given inequality.
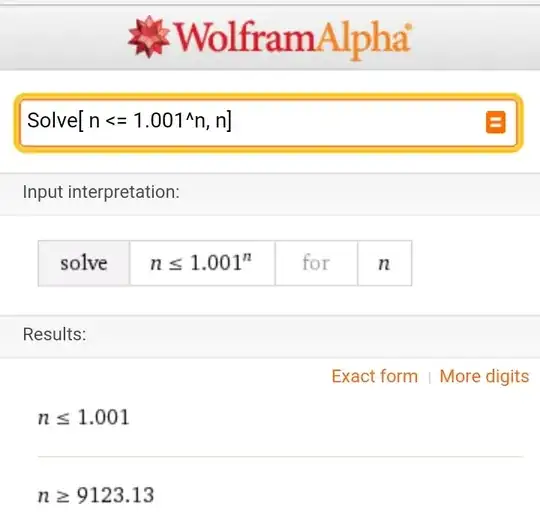
As a small example, we set $\epsilon = 0.001$ and ask mathematica to find our answer:
meaning your lower bound is $9123.13$ or that your delta is $\delta = \frac{1}{9123.13} $
RGS
- 9,719