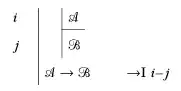2

I have a quick question regarding the introduction rule for the conditional: do you always need to proceed from an assumption or could you start from a premise? If so, then how would you go about it?

I need to prove the following formula using natural deduction: ¬Q ∧ ¬P ˫ ¬P → (R → ¬Q)

I've also made a quick proof.

1 (1) ¬Q ∧ ¬P       P 

2 (2) ¬P            A

3 (3) R             A

1 (4) ¬Q            1∧E

1 (5) R → ¬Q        1,3 →I

1 (6) ¬P → (R →¬Q)  2, 5 →I

I'm just wondering whether I have to assume ¬P in (2), when I already have it in (1)? Would it mean that ¬P is perfectly superfluous for the argument? That would seem to follow from the paradoxes of material implication (e.g B ˫ A → B).

Frank Hubeny
  • 1,527
William
  • 29
  • 2
    You have not to assume $\lnot P$. You have to use $\land$-elim on the premise (1) unpacking it into : (2) $\lnot Q$ and (3) $\lnot P$ and they are not assumptions, because they have been derived from (1). – Mauro ALLEGRANZA Nov 16 '16 at 11:23
  • 1
    Regarding the "paradox" of material implication : yes, $Q \vdash P \to Q$ with $P$ whatever. "Intuition" : $\vDash Q \to (P \to Q)$. – Mauro ALLEGRANZA Nov 16 '16 at 12:12
  • Thanks for the answer! The formulation of →Introduction just always mentions P as an assumption. So i could go (2) ¬P 1∧E and then in (6) ¬P→(R→¬Q) 2, 5 →I? That would be a perfectly acceptable use of →Int? – William Nov 16 '16 at 15:29
  • @William Your proof looks fine to me. – DanielV Nov 16 '16 at 21:35
  • I suggest you look at the examples I list at http://math.stackexchange.com/a/1788516, where I use Fitch-style notation to make the scope of 'assumptions' clear. I strongly discourage using any notation that does not make this clear. – user21820 Nov 17 '16 at 08:51

2 Answers2

1

It depends on the proof system and how exactly it has formally defined its formal inference rules.

If your particular proof system insists on making an explicit distinction between premises and assumptions, and if it insists on having the $\rightarrow I$ rule only use assumptions for the antecedent, then no, you can't use a premise.

But, in terms of pure logic, it should of course work just as well whether you use an assumption or a premise for a conditional proof: in both cases, the assumption base will tell you where the derived statement comes from. Indeed, most systems really don't make any explicit difference between premises and assumptions. So then your proof could be done like this:

1 (1) ¬Q ∧ ¬P       A 

1 (2) ¬P            1∧E

2 (3) R             A

1 (4) ¬Q            1∧E

1 (5) R → ¬Q        3,4 →I (you had a little mistake in line numbers here)

1 (6) ¬P → (R → ¬Q) 2,5 →I

Since line 6 shows that ¬P → (R → ¬Q) is a logical consequence of ¬Q ∧ ¬P, you can conclude ¬Q ∧ ¬P ˫ ¬P → (R → ¬Q)

Bram28
  • 100,612
  • 6
  • 70
  • 118
1

In this Fitch-style natural deduction proof checker I would have to assume $\neg P$ to derive a conditional with $\neg P$ as the antecedent. This depends on the definition of the inference rule for conditional introduction ($\to$I). Here is what that definition looks like from the proof checker's page:

enter image description here

To derive a conditional sentence, I have to make an assumption at the top of a subproof above the horizontal line, derive the consequent, and then I am permitted to close the subproof to derive the conditional.

Here are the questions:

I'm just wondering whether I have to assume $\neg P$ in (2), when I already have it in (1). Would it mean that $\land \neg P$ is perfectly superfluous for the argument?

In this proof checker you would have to assume $\neg P$ even though you have it as a premise. A conditional is not a claim that you know the truth value of the antecedent. It only claims that assuming the antecedent you can derive the consequent which is what the subproof showed.

Here is a proof:

enter image description here

Note that I only needed the premise for $\neg Q$ on line 4 because I had to derive that line. I did not have to derive the lines 2 and 3. They started subproofs each with an assumption.

Kevin Klement's JavaScript/PHP Fitch-style natural deduction proof editor and checker http://proofs.openlogicproject.org/

Frank Hubeny
  • 1,527