Two cuts are made in a random fashion on a line which length is 1 ft. What is the probability that at least one of the resulting segments (pieces) will be more than 0.5 ft? And why?
Asked
Active
Viewed 140 times
-1
-
Similar to http://math.stackexchange.com/questions/26424/a-samurai-cuts-a-piece-of-bamboo (since if all three lengths are less than $\frac12$ then you can form a triangle) – Henry Nov 15 '16 at 19:51
1 Answers
0
Comment: First, look into @Henry's Comment.
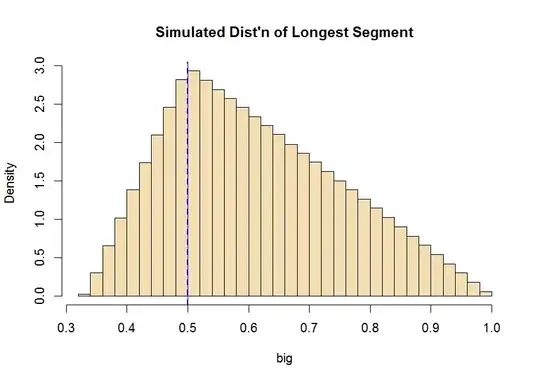
Second, here is a simulation in R statistical software of ten million performances of the two-cut experiment. The probability that the longer segment is longer than 1/2 seems to be 3/4.
I have shown details of the first six simulated experiments (rounded to fit the page). Maybe this information will help you think through the analysis more clearly.
m = 10^7
c1 = runif(m); c2 = runif(m) # two random cuts
mn = pmin(c1, c2); mx = pmax(c1, c2) # min and max dist from left side
x1 = mn; x2 = mx - mn; x3 = 1-mx # lengths of three pieces
big = pmax(x1, x2, x3) # longest of three pieces
round(head(cbind(c1,c2, mn,mx, x1,x2,x3, big)),3) # show first few results
c1 c2 mn mx x1 x2 x3 big
[1,] 0.559 0.402 0.402 0.559 0.402 0.157 0.441 0.441
[2,] 0.728 0.350 0.350 0.728 0.350 0.378 0.272 0.378
[3,] 0.983 0.006 0.006 0.983 0.006 0.977 0.017 0.977
[4,] 0.830 0.347 0.347 0.830 0.347 0.483 0.170 0.483
[5,] 0.552 0.405 0.405 0.552 0.405 0.147 0.448 0.448
[6,] 0.814 0.257 0.257 0.814 0.257 0.557 0.186 0.557
mean(big > .5)
## 0.7501509
BruceET
- 51,500