5

Question: How many routes are there from $A$ to $B$ along the grid in the diagram below? You can only move upwards or to the right until you reach $B$.

Diagram 1 I started off by listing some paths that will get me to $B$. I started listing them off...\begin{align*} & \text{UUURRUURRUURRR}\\ & \text{UUURRRUURUURRR}\\ & \text{UURRUUURRURRRU}\\\vdots\end{align*} Soon, I realized that this was a simple counting problem. So I got$$\binom{14}{7}=\text{Some large number greater than 2000}$$ But the answer was exactly $2000$. Where did I go wrong?

Hypergeometricx
  • 22,657
Frank
  • 5,984
  • you are going further, see that the path RRRRRRRUUUUUUU is possible in the binomial but not in the graph – Phicar Nov 14 '16 at 03:38
  • @Phicar Ooohhh.... Then how would you solve this? – Frank Nov 14 '16 at 03:43
  • Do the same analysis but you have to go to the cut points of the graph, say $(4,3),(3,4)$(read them as it where in the plane) etc..You have to pass by those points. – Phicar Nov 14 '16 at 03:50
  • 1
    Also notice that there is a symettry by the middle So just do it to the cut points below the diagonal and multiply by 2. You will end up with something like $2\binom{5}{3}^3$ – Phicar Nov 14 '16 at 03:54
  • @Phicar - Very nice closed form. You should post this as a solution. – Hypergeometricx Nov 15 '16 at 08:50

3 Answers3

4

Setting A in the origin $(0,0) $, we must necessarily pass through either the point $C=(3,2)\, $ or the point $D=(2,3)\, \, $. Similarly, we must also necessarily pass through either the point $E=(5,4) \,\,$ or the point $F=(4,5) \,\,$.

The pathways that cross $C $ and $E $ are $\binom{5}{3} \binom{4}{2} \binom{5}{3} =600 \, \,\, \,$, whereas those crossing $C $ and $F $ are $\binom{5}{3} \binom{4}{1} \binom{5}{3} =400\, \, \,$. So, a total of $1000$ paths pass through $C $. Due to the symmetry of the problem the number of paths passing through $D $ is equal. So we have a total of $2000$ paths.

Anatoly
  • 17,079
4

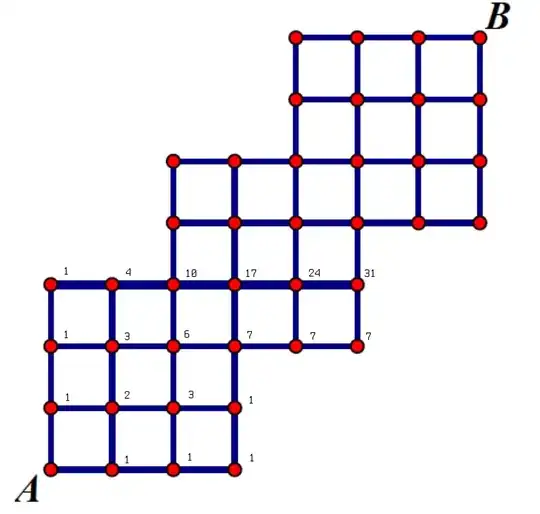
$\hspace{2cm}$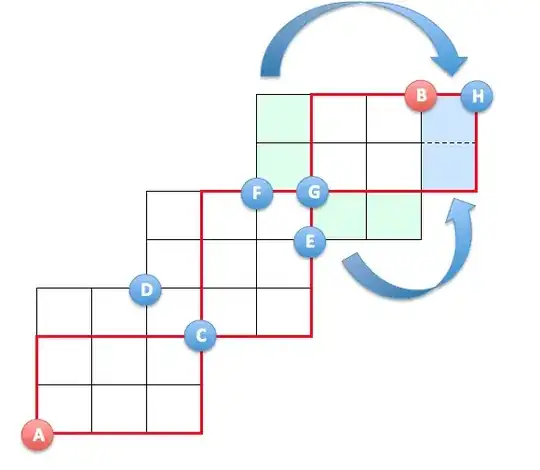enter image description here

Refer to the diagram above.

Denote $\vec{XY}_Z$ as the number of ways to move from point $X$ to point $Y$ moving through optional point $Z$. We want to find $\vec{AB}$.

First we consider the number of paths through $C$, i.e. $\vec{AB}_C$. The problem can be simplified by superimposing several $2\times 3$ hexominoes (shown in red) on the original and extended lattice.

$\vec{AB}_C$ can be computed as a product of several subpaths as follows (* indicates multiply): $$\vec{AB}_C=\vec{AC}*\left[\vec{CE}* \vec{EB}+\vec{CF}*\vec{FB}\right]$$

Note that

  • $\vec{CE}+\vec{CF}=\vec{CG}$ (by symmetry and also because $G$ is one step away from $E,F$) and

  • $\vec{FB}=\vec{EB}=\vec{GH}$ (moving green squares to blue squares on lattice extension).

Hence $$\vec{AB}_C=\vec{AC}*[(\vec{CE}+\vec{CF})*\vec{GH}]=\vec{AC}*\vec{CG}*\vec{GH}=\binom 52^3$$

By symmetry along diagonal $AB$, it is obvious that $\vec{AB}_D=\vec{AB}_C$. A similar but orthogonal set of hexominoes can be drawn for $\vec{AB}_D$.

Hence the total number of paths from $A$ to $B$ is given as

$$\vec{AB}=\vec{AB}_C+\vec{AB}_D=\color{red}{2\binom 52^3=2000}$$

General Case

For a similar configuration of $3$ lattices each of dimension $n\times n$ and overlapping by one square along a common diagonal, the number of paths from the lowest leftmost point to the highest rightmost point is given by $$2\binom {2n-1}{n-1} ^3$$

It can also be shown that for a similar configuration of $m$ attices each of dimension $n\times n$ and overlapping by one square along a common diagonal, the number of paths from the lowest leftmost point to the highest rightmost point is given by $$2\binom {2n-1}{n-1} ^m$$

Hypergeometricx
  • 22,657
1

EDIT: I got some of the numbers wrong below and am too lazy to fix them, but the general principle still applies.

enter image description here

I'd do it the old fashioned way and just compute the number of paths to each point (by adding the number of ways to the points "west" and "south" of each node) until I reached B. I've done roughly half above.