4

Is there a proof that will convince someone who doesn't understand calculus, of $\pi$'s irrationality .

Vincenzo Tibullo
  • 10,955
user13107
  • 417
  • I don't believe anyone has discovered any such proof yet. –  Sep 23 '12 at 09:13
  • $\pi$ is irrational iff the orbit of $(1,0)$ under rotations of angle $1$ is dense in the circle; so maybe you can convince someone that $\pi$ is irrational by drawing approximations of this orbit (of course, it is not a proof). – Seirios Sep 23 '12 at 09:29
  • @Seirios Sorry, I'm not getting you. A figure maybe? – user13107 Sep 23 '12 at 09:37

2 Answers2

3

As far as I know, there aren't any simpler proofs. And because pi is transcendental, it doesn't seem like the proof would lend itself well to anything easier than calculus.

Joe Wells
  • 1,110
  • Ok. May be not easier than calculus, but how about something different than calculus? – user13107 Sep 23 '12 at 09:22
  • 7
    My first thought was that you could prove that $\pi$ is transcendental, which would be sufficient, but that explanation would take much longer and would probably be less satisfying for those who don't have the necessary abstract algebra background.

    Lambert's proof uses continued fractions and essentially concludes that if $\tan(x)$ is rational, then x is irrational. Since $\tan \left( \frac{\pi}{4} \right) = 1$, then $\frac{\pi}{4}$ is irrational. I haven't really looked into it, but it might be more accessible.

     – Joe Wells Sep 23 '12 at 09:40
  • Cool, thanks for the pointers. Sorry, can't vote up w/o rep. – user13107 Sep 23 '12 at 09:56
  • 2
    In a similar vein, no one seems to know a proof that $\pi$ is not constructible without proving that it is transcendental. See http://math.stackexchange.com/questions/103786/direct-proof-that-pi-is-not-constructible – lhf Sep 23 '12 at 11:32
  • $e$ is transcendental, but if you accept $e=\sum^{\infty}(n!)^{-1}$, you can prove it irrational without Calculus. Also $.1101001000100001000001\dots$ is transcendental, but its irrationality is trivial and no Calculus is needed. – Gerry Myerson Sep 23 '12 at 12:26
  • @GerryMyerson isn't that representation of $e$ built on calculus? infinite (specifically taylor) series seems to be directly from calculus...unless of course the OP meant modulo integral/differential calculus... – Coffee_Table Jul 21 '14 at 22:33
  • @Coffee, I don't think I was responding directly to the original question, but to some comment, possibly to some comment that has since been deleted. Taylor series certainly presupposes Calculus, but one can do a lot with infinite series without any Calculus (though you do need limits). As for $e$, it is possible to take that infinite series as the definition of $e$, and if you take that approach then no Calculus is needed to prove irrationality. – Gerry Myerson Jul 22 '14 at 00:03
  • @GerryMyerson I hear that. I guess I just always associate certain studies of the "infinite"-i.e., series and limits-with calculus, but I guess there's no reason for that to be set in stone, and it is my own bias. Also, I just saw the date on your comment! It just happens to be that I recently became interested in this very question and my googling led me directly here... – Coffee_Table Jul 22 '14 at 02:23
  • @GerryMyerson You can define $e$ without calculus, if you want: The unique number $e$ such that $e^x\ge x+1$ for all $x$. (This definition is surprisingly powerful. It lets you prove that $x^x$ has a minimum at $e^{-1}$, for example, and it lets you prove that $1-\frac12+\frac13-\dotsb=\ln2$. This is all without using calculus. EDIT: Well, technically, you just get to prove that $\ln2-\frac1n<1-\frac12+\dotsb\frac1n<\ln2+\frac1n$, but the Squeeze Theorem implies the infinite version immediately. I suppose that the Squeeze Theorem is kinda calculus-y, but not too calculus-y.) – Akiva Weinberger Apr 03 '15 at 11:16
  • @colum, OK, though somehow you have to prove that there exists a unique number such that $\forall x, e^x\ge x+1$. – Gerry Myerson Apr 06 '15 at 10:47
  • @GerryMyerson Yeah, yeah, but playing with desmos.com (graphing calculator) shows that it's pretty likely. (Graph x+1 and a^x, and then adjust the value of a.) – Akiva Weinberger Apr 06 '15 at 11:49
2

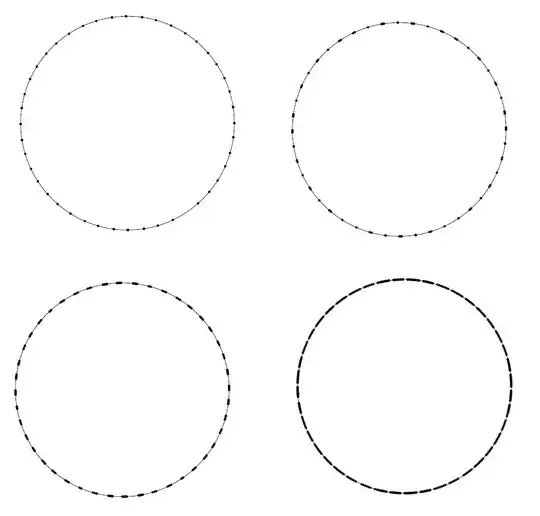
I developp my comment: Take the point $x_0=(1,0)$ on the unit circle $S^1$; if $R$ is the rotation of one radian around $(0,0)$, let $x_1=Rx_0$, $x_2=Rx_1$, $x_3=Rx_2$ and so on.

In complex notation, you have $x_n=e^{in}$. If $\pi$ is rational, there exist $p,q>0$ such that $\pi=p/q$ and so $x_{2p}=e^{i2p}=e^{i2q\pi}=x_0$; thus, $\{x_n, n \geq 0\}$ is discrete in $S^1$. Otherwise, $\{x_n,n \geq 0\}$ is dense in $S^1$, ie. it seems to cover the circle.

Consequently, you can convince someone without calculus that $\pi$ is irrational by showing that $\{x_n, \geq 0\}$ seems to cover the circle; of course, it is not a proof.

Here are some iterations:

Density in the circle

Seirios
  • 33,157