The ellipse $E$ has eccentricity $\frac{1}{2}$, focus $(0,0)$ with the line $x=−1$ as the corresponding directrix. Find an equation for $E$.
The equation I get is $(x+\frac{1}{3})^2 + y^2=\frac{4}{9}$ which is a circle, radius $\frac{2}{3}$. Is this wrong? I feel it must be because I then have to find the other focus and directrix.
Let's do this step by step.
\begin{align*} \lvert PF\rvert &= e\,\lvert PL\rvert \\ \lvert PF\rvert^2 &= e^2\,\lvert PL\rvert^2 \\ x^2+y^2 &= \left(\tfrac12\right)^2(x+1)^2 \\ 4x^2+4y^2 &= x^2+2x+1 \\ 3x^2-2x+4y^2 &= 1 \\ 3\left(x^2-2x\cdot\tfrac13+\tfrac19\right) + 4y^2 &= 1+3\cdot\tfrac19 \\ 3\left(x-\tfrac13\right)^2 + 4y^2 &= \tfrac43 \\ \tfrac94\left(x-\tfrac13\right)^2 + 3y^2 &= 1 \\ \left(\frac{x-\tfrac13}{\tfrac23}\right)^2 + \left(\frac{y-0}{\sqrt{\tfrac13}}\right)^2 &= 1 \end{align*}
So the center would be at $(\tfrac13,0)$, the length of the semiaxis in $x$ direction would be $\tfrac23$ and the length of the semiaxis in $y$ direction would be $\sqrt{\tfrac13}$. The grid in the following illustration has distance $\tfrac13$ between the lines.
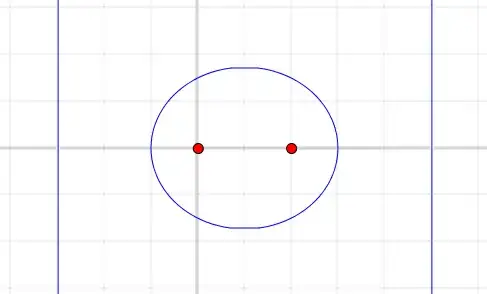
Note that the above computation heavily relies on the fact that the directrix is vertical, which makes the whole ellipse axis-aligned. Otherwise we'd have to account for rotation, which would complicate things. See this post of mine for reading geometric properties of a generic equation. In the case of a focus and directrix description, it would be easier to first transform coordinates to axis-align the directrix, though.
I'm not sure how you obtained your equation, so I can't tell you where you went wrong.
