1

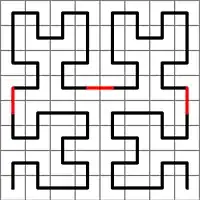
Is anyone aware of a space-filling curve where two points "near" each other in 2D are "near" each other when the curve is extended? This relationship doesn't seem to hold with the Hilbert curve: when two points are near each other on the curve they're near each other in 2D space, but not necessarily vice versa.

See the below image, for example. The two pixels at the bottom-center of the square are right next to each other in 2D, but when you "stretch out" the curve into 1D, they are very far apart.

enter image description here

Alternatively, can someone prove that no such mapping exists?

Mark McClure
  • 30,510
Andrew Watson
  • 145
  • Interesting question, though, we might need to be careful to make it precise. To say that $A$ and $B$ are "near each other on the curve", I suppose we might mean that their pre-images (ie. the points $t_1$ and $t_2$ that map to $A$ and $B$) are near each other. Does that seem reasonable? If so, I think this cannot happen. In fact, no space-filling curve can be one-to-one. Thus, there will always be distinct points $t_1$ and $t_2$ that map to the same point on the curve. The distortion is then essentially infinite. – Mark McClure Nov 07 '16 at 00:41

1 Answers1

1

The fact that such a curve can't be injective seems to contradict what you are looking for. Two different points on the line are sent to the same point in the square and are thus made 'perfectly close' but they are different points on the line so are not 'perfectly close'.

Community
  • 1
Chessanator
  • 5,448