My teacher proved that following formula is not tautology in intuitionistical logic:
$$\neg(p\wedge q)\Leftrightarrow (\neg p\vee\neg q)$$
Is it sufficient to show (and we try to do it) that $$\neg(p\wedge q)\Rightarrow (\neg p\vee\neg q)$$ is not tautology.
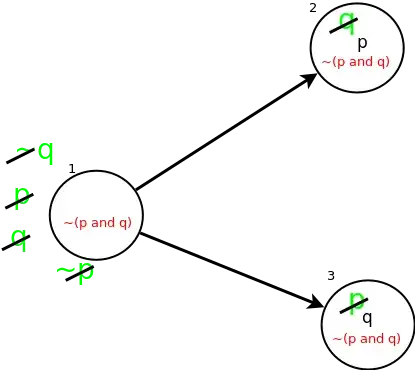
My teacher wrote red and black formulas. My formulas are green - there are formulas that to my eye my teacher forgot to write.
I know that teacher give arbitrar Kripke model. Tell me please:
1. If my green "supplement" is correct ?
2. From what my teacher conclude red formulas ? When it comes to black things I know that it is about kripke model.
Asked
Active
Viewed 49 times
1
-
To my limited knowledge, it is a tautology. – Nitin Uniyal Nov 06 '16 at 08:33
-
@mathlover, even in intuitonistical logic ? – Nov 06 '16 at 08:54
-
In intuitionistic logic, whenever the claim $A \lor B$ is present, you always know which is true. So from $\lnot(A \land B)$ you know that you can't construct both...but you don't know which one can't be constructed. It could be that $A$ is not constructible, it could be that $B$ is not constructible, or it could be that both aren't. You can't deduce $\lnot A \lor \lnot B$ because you aren't given enough information to know which isn't constructible. That's obviously not a formal proof, just some intuition behind why that direction doesn't work. – DanielV Nov 06 '16 at 11:56
-
tell me please If I correctly write green formulas. – Nov 06 '16 at 11:57