6

In the Poincare Disk Model, Hyperbolic circles (i.e. the locus of all points with a given distance from a center point) are also circles in the euclidean sense, but with the euclidean center different from the hyperbolic center.

My question is, given a known hyperbolic center point and hyperbolic radius, how can one find the euclidean center and radius of the hyperbolic circle?

Either a geometric construction or a simple analytical formula will do.

To clarify: You are only given the radius length, not a point on the circle. There is no constraint on what you are allowed to use in your solution: Analytic solutions are perfectly acceptable. In the diagram: Given the point $A$ and a hyperbolic distance, find the point $B$ and the euclidean radius of the circle.

$\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space$enter image description here

Nathaniel Bubis
  • 33,018

2 Answers2

4

Making my comment more explicit ...

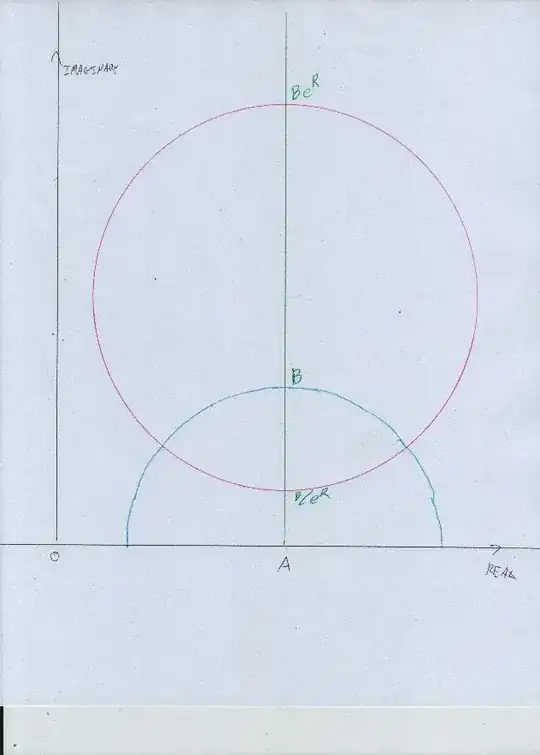
Writing $|\cdot|$ for Euclidean distance, and $|\cdot|^\star$ for hyperbolic distance, we have a relatively simple relation for distances from the origin:

$$|OX|^\star = \log\frac{1 + |OX|}{1 - |OX|} = 2 \operatorname{atanh}|OX| \qquad\qquad |OX| = \tanh\frac{\;|OX|^\star}{2} \tag{$\star$}$$

Let the diameter of the target circle meet $\overleftrightarrow{OA}$ at $P$ and $Q$, and define $a := |OA|$, $p := |OP|$, $q := |OQ|$, with $a^\star$, $p^\star$, $q^\star$ their hyperbolic counterparts. Let $r^\star$ be the target circle's hyperbolic radius.

We may assume $p \geq a$ (one of the diameter's endpoints must be on the "far side" of center $A$), so that

$$p^\star = a^\star + r^\star \quad\to\quad p = \tanh\frac{a^\star + r^\star}{2} = \frac{(1+a)\exp r^\star - (1 - a)}{(1+a)\exp r^\star + ( 1 - a)} \tag{1}$$

For the other endpoint, $Q$, an ambiguity arises based on whether the origin lies outside or inside the circle, but we have

$$q^\star = \pm ( a^\star - r^\star ) \quad\to\quad q = \pm \tanh\frac{a^\star - r^\star}{2} = \pm \frac{(1+a) - ( 1 - a )\exp r^\star}{(1+a) + (1-a)\exp r^\star} \tag{2}$$

where "$\pm$" is "$-$" for $O$ inside the circle, and "$+$" otherwise. (If you like, you can absorb the sign into the distances $q$ and $q^\star$, so that they are negative when $\overrightarrow{OA}$ and $\overrightarrow{OQ}$ point in opposite directions, and positive otherwise.)

With the endpoints of the target circle's diameter known, determining the Euclidean center and Euclidean radius is straightforward. $\square$

Note. If $R$ is such that $|OR|^\star = r^\star$, and if we define $r := |OR|$, then $(1)$ and $(2)$ become:

$$p = \frac{a + r}{1 + a r} \qquad\qquad q = \pm \frac{a - r}{1 - a r} \tag{3}$$

Blue
  • 75,673
2

To map (isometrically) from the unit disc to the upper half plane, $$ \frac{z + i}{i z + 1} $$ In the upper half plane, the following is a unit speed geodesic: $$ t \mapsto A + i e^t. $$ Your circle center goes somewhere, call the real part $A,$ the imaginary part $e^{t_0}.$ This is the geometric mean of the highest point (imaginary part $e^{t_2},$ say) and the lowest point.

Trying again: the center is mapped to $A + i B,$ with real $A,B$ and $B > 0.$ You want some "hyperbolic radius," call that $R.$ The point on the circle with real part $A$ and higher than $B$ has imaginary part $B e^R.$ The point on the circle with real part $A$ and lower than $B$ is $B/ e^R.$ These three points lie on a diameter, both as "hyperbolic" objects and Euclidean ones. I did not mark in the "Euclidean" center in the diagram, it is at $A + i B \cosh R.$

enter image description here

To map back from the upper half plane to the unit disc, $$ \frac{iz + 1}{ z + i} $$

Will Jagy
  • 139,541