Rigorous definition of "differential"

Question

When it comes to definitions, I will be very strict. Most textbooks tend to define differential of a function/variable like this:

---

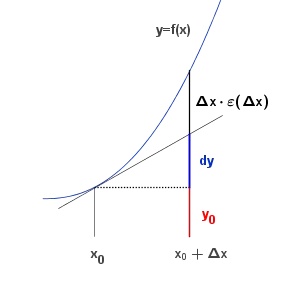
Let $f(x)$ be a differentiable function. By assuming that changes in $x$ are small enough, we can say: $$\Delta f(x)\approx {f}'(x)\Delta x$$ Where $\Delta f(x)$ is the changes in the value of function. Now we define differential of $f(x)$ as follows: $$\mathrm{d}f(x):= {f}'(x)\mathrm{d} x$$ Where $\mathrm{d} f(x)$ is the differential of $f(x)$ and $\mathrm{d} x$ is the differential of $x$.

---

What bothers me is this definition is completely circular. I mean we are defining differential by differential itself. Can we define differential more precisely and rigorously?

P.S. Is it possible to define differential simply as the limit of a difference as the difference approaches zero?: $$\mathrm{d}x= \lim_{\Delta x \to 0}\Delta x$$ Thank you in advance.

---

EDIT:

I still think I didn't catch the best answer. I prefer the answer to be in the context of "Calculus" or "Analysis" rather than the "Theory of Differential forms". And again I don't want a circular definition. I think it is possible to define "Differential" with the use of "Limits" in some way. Thank you in advance.

---

EDIT 2 (Answer to "Mikhail Katz"'s comment):

the account I gave in terms of the hyperreal number system which contains infinitesimals seems to respond to your concerns. I would be happy to elaborate if anything seems unclear. – Mikhail Katz

Thank you for your help. I have two issues:

First of all we define differential as $\mathrm{d} f(x)=f'(x)\mathrm{d} x$ then we deceive ourselves that $\mathrm{d} x$ is nothing but another representation of $\Delta x$ and then without clarifying the reason, we indeed treat $\mathrm{d} x$ as the differential of the variable $x$ and then we write the derivative of $f(x)$ as the ratio of $\mathrm{d} f(x)$ to $\mathrm{d} x$. So we literally (and also by stealthily screwing ourselves) defined "Differential" by another differential and it is circular.

Secondly (at least I think) it could be possible to define differential without having any knowledge of the notion of derivative. So we can define "Derivative" and "Differential" independently and then deduce that the relation $f'{(x)}=\frac{\mathrm{d} f(x)}{\mathrm{d} x}$ is just a natural result of their definitions (using possibly the notion of limits) and is not related to the definition itself.

I know the relation $\mathrm{d} f(x)=f'(x)\mathrm{d} x$ always works and it will always give us a way to calculate differentials. But I (as an strictly axiomaticist person) couldn't accept it as a definition of Differential.

---

EDIT 3:

Answer to comments:

I am not aware of any textbook defining differentials like this. What kind of textbooks have you been reading? – Najib Idrissi

 

which textbooks? – m_t_

Check "Calculus and Analytic Geometry", "Thomas-Finney", 9th edition, page 251

and "Calculus: Early Transcendentals", "Stewart", 8th edition, page 254

They literally defined differential by another differential.

Answer 1

Of course, defining $$ \mathrm{d}x= \lim_{\Delta x \to 0}\Delta x $$ is the same as defining $$ dx=0, $$ which makes no sense. The correct approach is to define the differential as a kind of linear function: the differential $df(x)$ (sometimes denoted by $df_x$) is the linear function defined by $$ df(x):\mathbb R\to\mathbb R\qquad t\mapsto f'(x)\cdot t $$ In particular $$ dx:\mathbb R\to\mathbb R\qquad t\mapsto t $$ Therefore, one can also write $ df(x)=f'(x)dx$ (the composition with the identity map). This sounds perhaps trivial for scalar funtions $f$. The concept is more interesting for vector functions of vector variables: in that case $df(x)$ is a matrix. The differential $df(x_0)$ has to be interpreted as the best linear function which approximates the incremental function $h(x):=f(x)-f(x_0)$ near $x=x_0$. In this sense, the concept is connected to the idea you have expressed through the approximate 'equation' $\Delta f(x)\approx {f}'(x)\Delta x$

Answer 2

There are two ways of defining the differential of $y=f(x)$:

(1) as differential forms. Here $dx$ is a linear function on the tangent space (in this case tangent line) at a point, and the formula $dy=f'(x)dx$ is a relation between 1-forms.

(2) as an infinitesimal number. Such a number is an element of the hyperreal number system, as detailed in the excellent textbook by H. J. Keisler entitled Elementary Calculus that we are currently using to teach calculus to 150 freshmen.

Here the independent variable $\Delta x$ is an infinitesimal, one defines $f'(x)=\textbf{st}(\frac{\Delta y}{\Delta x})$ where "$\textbf{st}$" is the standard part function (or shadow) and $\Delta y$ is the dependent variable (also infinitesimal when the derivative exists). One defines a new dependent variable $dy$ by setting $dy=f'(x)dx$ where $dx=\Delta x$. Note that it is only for the independent variable $x$ that we set $dx=\Delta x$ (therefore there is no circularity).

The advantage of this is that one can calculate the derivative $\frac{dy}{dx}$ from the ratio of infinitesimals $\frac{\Delta y}{\Delta x}$, rather than merely an approximation; the proof of the chain rule becomes more intuitive; etc.

More generally if $z=f(x,y)$ then the formula $dz=\frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y}dy$ has two interpretations: as a relation among differential 1-forms, or as a relation among infinitesimal differentials. Classical authors like Riemann interpreted such relations as a relation among infinitesimal differentials.

It is not possible to define $dx$ by a limit as in $\mathrm{d}x= \lim_{\Delta x \to 0}\Delta x$ (as you wrote) because that would simply be zero, but a generalisation of limit called ultralimit, as popularized by Terry Tao, works just fine and produces an infinitesimal value for $dx$.

More specifically, concerning your hope of somehow "defining differentials with the help of limits", the following can be said. The notion of limit can be refined to the notion of an ultralimit by refining the equivalence relation involved in defining the limit. Thus the limit of a sequence $(u_n)$ works in such a way that if $(u_n)$ tends to zero then the limit is necessarily zero on the nose. This does not leave much room for infinitesimals. However, the refined notion, the ultralimit, of a sequence $(u_n)$ tending to zero is typically a nonzero infinitesimal, say $dx$. We can then use this as the starting point for all the definitions in the calculus, including continuity and derivative. The formula $dy= f'(x) dx$ then literally makes sense for nonzero differentials $dx$ and $dy$ (unless of course $f'(x)=0$ in which case $dy=0$).

The definition is not circular because the infinitesimal $\Delta y$ is defined as the $y$-increment $f(x+\Delta x)-f(x)$. This was essentially Leibniz's approach (differentials are just infinitesimals) and he rarely did things that were circular.

Answer 3

We consider a real valued function $y=f(x)$ differentiable at $x=x_0$.

The following reasoning can be found in section 3.7 of Höhere Mathematik, Differentialrechnung und Integralrechnung by Hans J. Dirschmid.

Definition: We call the change of the linear part of $f$ at $x=x_0$ considered as function of the argument increment $\Delta x$ the differential of the function $f$ at $x_0$, symbolically \begin{align*} dy=f^\prime(x_0)\Delta x\tag{1} \end{align*} The linear part of $f$ at $x_0$ is the expression \begin{align*} f(x_0)+f^\prime(x_0)\Delta x \end{align*}

Note that we introduce the term $dy$ in (1) without using $dx$ and so avoid any circular reasoning.

Here is a small figure for illustration:

                                        

When talking about the differential $dy$ we use it for both as a function symbol and as the value of the function $dy$ evaluated at $\Delta x$. \begin{align*} dy=dy(\Delta x)=f^\prime(x_0)\Delta x\tag{2} \end{align*}

$$ $$

Connection with $dx$:

We consider the identity function $y=x$. Since $y^\prime=1$ we obtain by (2) \begin{align*} dy=1\cdot \Delta x=\Delta x \end{align*} Since $y=x$ and $dy=\Delta x$ we use this relationship to define \begin{align*} dx:=\Delta x \end{align*} and call it the differential of $x$.

With this two step approch we can write $dy=f^\prime(x_0)\Delta x$ as \begin{align*} dy=f^\prime (x_0) dx\tag{3} \end{align*} and resolve the seemingly circular definition.

[Add-on 2016-11-15]:

From (3) we see the differentials $dy$ and $dx$ are proportional as functions of $\Delta x$. Since we are allowed to divide real functions, we can also consider the quotient \begin{align*} \frac{dy}{dx}=f^\prime(x_0)\tag{4} \end{align*} This justifies the term differential quotient.

Observe the left-hand side of (4) is the quotient of two functions dependent on the argument increase $\Delta x$ which does not occur on the right-hand side. This implies that the quotient does not depend on the argument $\Delta x$ of the numerator $dy$ and the denominator $dx$.

$$ $$

Approximation of $f$ at $x=x_0$:

The linear part $$f(x_0)+f^\prime(x_0)\Delta x$$ approximates the function $f$ at $x=x_0$ with an error which decreases with an order higher than first order. This implies the change of the linear part - the differential $dy$ - approximates the change of the function, which is the difference $\Delta y=f(x+\Delta x)-f(x)$ also with this error quality: \begin{align*} \Delta y=dy+\Delta x \varepsilon(\Delta x),\qquad \lim_{\Delta x\rightarrow 0}\varepsilon(\Delta x)=0. \end{align*}

Answer 4

I think the differential forms version deserves to be fleshed out a little more:

Let $x, y, z, \ldots$ be all the (scalar) variables in use. Write $p$ for a tuple that assigns values to those variables: $(x_p, y_p, z_p, \ldots)$. Then a variable quantity is a (mathematical) function that assigns a (real or vector) value to each tuple $p$. Note that the variables are well-defined variable quantities given by

$$x(x_p, y_p, z_p, \ldots) = x_p\\ y(x_p, y_p, z_p, \ldots) = y_p\\ z(x_p, y_p, z_p, \ldots) = z_p\\ \vdots$$

For each variable quantity $E$, we're going to define another quantity $dE$. In particular, if $E$ is a real variable quantity, the differential of $E$ $dE$ is going to be a (partial function) that assigns to each assignment $p$ a linear transformation from the vector space of assignments to the vector space of real numbers (under addition). If $E$ is a vector variable, $dE$ will map each $p$ to a linear transformation from the vector space of assignments to the vector space where $E$ takes its values (this is a generalization of the definition for real variables).

If $\Delta p$ is a small displacement of the assignment $p$, we want $E(p) + dE(p)\Delta p$ to be a good approximation to $E(p + \Delta p)$. Note first that $$dE(p)\Delta p \to 0 \text{ as } \Delta p \to 0$$ by definition, since we want $dE(p)$ to be linear. So unless $$E(p + \Delta p) \to 0 \text{ as } \Delta p \to 0$$ i.e., $E$ is continuous, $E(p) + dE(p)\Delta p$ is never going to be a good approximation to $E(p + \Delta p)$. So we're going to only look at points $p$ where $E$ is continuous (there may not be any such points).

On the other hand, $$E(p) + Q\Delta p \to E(p) \text{ as } \Delta p \to 0$$ for all linear transformations $Q$, so that can't be a sufficient definition of $dE(p)$. Consider the following: $$x \to 0 \text{ as } x \to 0\\ x^2 \to 0 \text{ as } x \to 0$$, but $$\frac{x}{x} \to 1 \text{ as } x \to 0\\ \frac{x}{x^2} \to \infty \text{ as } x \to 0\\ \frac{x^2}{x} \to 0 \text{ as } x \to 0$$ Intuitively, you can see that $x$ and $x^2$ go to 0 at different speeds as $x \to 0$. We can use that idea to pin down $dE(p)$ more precisely. At a minimum, we want $E(p) + dE(p)\Delta p$ to go to $E(p)$ faster than $\Delta p$ goes to 0. We can write this formally (rigorously) as $$\frac{E(p + \Delta p) - E(p) - dE(p)\Delta p}{\|\Delta p\|} \to 0 \text{ as } \Delta p \to 0$$ Note that this is precisely the same thing as defining $dE(p)$ to be the (vector) derivative of $E$ at $p$. The uniqueness of the linear transformation (if it exists) satisfying that property (the best linear approximation to $E$ at $p$) is a basic theorem proven in any vector analysis textbook.

The variable quantity $f(x)$ is really a composition: $f(x)(p)$ really means $f(x(p))$. So the rule $$d(f(x)) = f'(x)dx$$ (which really means $$d(f(x))(p) = f'(x(p))(dx(p))$$) is just a simple application of the chain rule.

Answer 5

You may find some useful answers with similar (?) MSE questions:

• Why do we treat differentials as infinitesmals, even when it's not rigorous
• Differential and Infinitesimals
• Learning differential calculus through infinitesimals
• What are the grounds for treating 'dx(differential, infinitesimal)' as if they were numbers?
• Infinitesimal calculus
• When can't $dy/dx$ be used as a ratio/fraction?

Answer 6

What bothers me is this definition is completely circular. I mean we are defining differential by differential itself. Can we define differential more precisely and rigorously?

What book are you reading and where did you find such definition? Since you mentioned Stewart in your post, I would like to mention that the version he gave in his calculus book is not circular:

---

[Added later:] In Stewart's definition, he is using the differential of $x$ to define the differential of $y$, which is not circular because they are two different things in the definition: first of all you define $dx$ to be $\Delta x$, which is a real number and call it the "differential of $x$"; then you define "the differential of $y$ (at $x$)" be $f'(x)\ dx$ and denoted it as $dy$.

---

First of all we define differential as $\mathrm{d} f(x)=f'(x)\mathrm{d} x$ then we deceive ourselves that $\mathrm{d} x$ is nothing but another representation of $\Delta x$

No. It is the other way around in Stewart's definition. He defines $dx$ to be $\Delta x$ first.

and then without clarifying the reason, we indeed treat $\mathrm{d} x$ as the differential of the variable $x$

Again, it is the other way around. First $dx$ is defined, then it is called the differential of $x$.

and then we write the derivative of $f(x)$ as the ratio of $\mathrm{d} f(x)$ to $\mathrm{d} x$. So we literally (and also by stealthily screwing ourselves) defined "Differential" by another differential and it is circular.

No. The notation $\frac{dy}{dx}$ is not defined by $dy$ and $dx$. The three notations $\frac{dy}{dx}$, $dy$ and $dx$ are completely different things. You could say that this is an abuse of notation, but not circular.

---

I prefer the answer to be in the context of "Calculus" or "Analysis" rather than the "Theory of Differential forms". And again I don't want a circular definition. I think it is possible to define "Differential" with the use of "Limits" in some way.

• In the context of an undergraduate-level calculus course, I don't think you should expect a "rigorous" definition of differential of a function. In a "rigorous" analysis book, one would not even use the symbol "$\approx$". It seems that you don't doubt that an expression like $ \Delta y\approx f'(x)\Delta x $ is actually not rigorous.

• The trouble to define the differential of a function is that the mathematical object "$dx$" and "$dy$" is not even a real number. (By the way, I don't think any calculus book would tell you what a real number really is.) One might appreciate the beauty and rigorousness of the $\epsilon$-$\delta$ definition of a limit so much that one might think that's the only way to make a mathematical concept rigorous. However, that is not the case. In an undergraduate linear algebra course, one would rarely see any argument using the $\epsilon$-$\delta$ language. Without knowing want a linear transformation is, (which, I would say, is the minimum requirement for giving a rigorous definition of differentials, if one dose not want to run to the so called non-standard analysis) one would hardly know what the differential of a function really is.

• If you want to read "rigourous" mathematics, a book like Stewart's one (good for an introduction though) would not be appropriate for you. You could try Analysis (I and II) by Terence Tao.

• As Terence Tao said: There’s more to mathematics than rigour and proofs.

Answer 7

My advice: Don't worry about it. I've always taught calculus without defining the damned things and done well with that approach. I of course push around differentials from time to time, as in changes of variables for integrals, but I introduce it with a public service announcement: this doesn't make literal sense, everybody, but let's use it as a convenient notational device.

Let me say I think $dy/dx$ as notation is great in some ways, and $\int_a^b f(x)\, dx$ is even better. It reminds you of where these objects of study come from. But the notation $dy/dx$ should be taken as a whole. It's not a quotient of anything, although in appearance it reminds one of the quotients $\Delta y/\Delta x.$ We should stop trying to carve $dy/dx$ into smaller pieces and leave it alone! (I once had a student who looked at $dx^2/dx$ on an exam, cancelled the $d$'s, then cancelled two $x$'s and obtained the answer of $x.$ I had to admit it had the right order of magnitude.)

To define $df$ as a linear mapping can confuse the heck out of students at the beginning. I remember self studying calculus out of Thomas back in the day, and I still have a copy of that book. Thomas tried to explain $df$ as this linear mapping thingie, and rereading it now, it seems like a joke, a terrible idea. That seems far removed from the original idea of $df$ as something "incredibly small".

Sure, in the more advanced setting of multivariable calculus, you'll see $df$ all over the place, denoting a certain linear mapping. That's a whole different ball of wax however. It's decent enough notation there, when you have experience, and when there is little chance of confusion with the original notions of differentials.

As for hyperreals and nonstandard analysis and all that, I am not qualified to say much. I've always been skeptical of this stuff. Seems to me to go beyond the "ghosts of departed quantities" to dark matter. But some mathematicians (not that many really) love this approach. Anyone going down this road should be advised that you will learn a language not too many of your peers and teachers will understand.

Answer 8

The differential of a function at a given point is the linear part of its behavior.

When you write $$f(x+dx)=f(x)+\Delta_f(x,dx),$$ the $\Delta_f$ has a linear part, i.e. strictly proportional to $dx$, which we can denote $dy=s\,dx$, where $s$ is a constant, and a remainder, let $\Delta'_f$.

Hence,

$$\Delta_f(x,d x)=s\,dx+\Delta'_f(x,dx)$$ where $\Delta'_f$ has a superlinear behavior at $x$ (quadratic or more). Thanks to this property, we can define $s$ by means of a limit, letting $\Delta'_f$ vanish:

$$s:=\frac{\Delta_f(x,dx)-\Delta'_f(x,dx)}{dx}=\lim_{dx\to0}\frac{\Delta_f(x,dx)}{dx}.$$

(In fact $s$ is defined when the limit exists.)

Of course, this definition coincides with that of the derivative, which allows us to write

$$dy=f'(x)\,dx.$$

Note that $dx,dy$ are not considered as "infinitesimals", but as finite numbers (variable but proportional to each other).