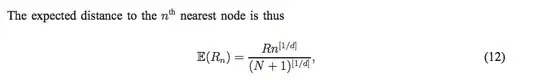3

Within a unit square, given n random uniform points, what is the average distance to the nearest k points? To be precise: if k=2 we are averaging the distances of the 1st and 2nd nearest neighbors to point i.

Here is a reference for the n=2 k=1 solution. Average distance between two randomly chosen points in unit square (without calculus) (for this question I assume calculus is needed)

However, if you rather had n points and were interested in the average distance to the k nearest neighbors is this something that can be solved with an exact answer?

I have produced results empirically for 10,000 iterations:

n=2, k=1: 0.52

n=3, k=2: 0.52 <- intuitively identical to n=2,k=1

n=5, k=4: 0.52 <- intuitively identical to n=2,k=1

n=3, k=1: 0.39

n=5, k=1: 0.28

n=10, k=1: 0.18

n=10, k=2: 0.24

n=10, k=3: 0.28

n=100, k=5: 0.097

Community
  • 1
rrbest
  • 163
  • For a given point, you mean the $k$th nearest neighbor without the plural. Is that so ? – Jean Marie Nov 01 '16 at 22:37
  • If k = 5 you would be return the average distance from all 5 nearest neighbors, not only the fifth nearest. – rrbest Nov 01 '16 at 22:48
  • This interpretation should be explained in your question... because it is not at all evident... – Jean Marie Nov 01 '16 at 22:50
  • 1
    When $n\gg k$, the distribution of points can be approximated by a Poisson process in the plane with density $n$. Then the number of other points in a ball of radius $r$ centered at a chosen point follows a Poisson distribution with rate parameter $\pi r^2n$. From this one could find the expected distance to the $i$th nearest neighbour, and thus, the expected average distance to the $k$ nearest neighbours, at least for the $n\gg k$ case. –  Nov 02 '16 at 01:04
  • I suppose the condition to avoid edge effects should be $\sqrt n\gg k$. In any case, for the $n=100,k=5$ case the Poisson process approximation gives $231/2560 \approx 0.0902$. –  Nov 02 '16 at 01:15

1 Answers1

2

Equation 12 in the paper

Distance Distributions in Finite Uniformly Random Networks: Theory and Applications

by Srinivasa and Haenggi, seems to answer your question:

Equation 12

Here is a simulation in MATLAB:

exps = 1000;
distances = zeros(exps,1);

N = 100;
k = 2;

for it=1:exps

    A = [ 2*(rand(5*N,1)-0.5) 2*(rand(5*N,1)-0.5)];
    A = A(sqrt(sum(A.^2,2)) <=1,:);
    A = A(1:N,:);

    B = [ 2*(rand(5*N,1)-0.5) 2*(rand(5*N,1)-0.5)];
    B = B(sqrt(sum(B.^2,2)) <=0.8,:); %There seems to be some problem on the edges
    B = B(1:N,:);


    [Idx,Dist] = knnsearch(A,B,'k',k);

   distances(it) =  mean(Dist(:,k));
end

experimental = mean(distances);

k = k;
analytic = (gamma(k + 0.5)/gamma(k))*( gamma(N + 1)/gamma(N + 1 + 0.5));

abs(experimental - analytic) # Gives 10^-4
The_Anomaly
  • 565