How to prove easily that a generalized ellipse is $C^1$

Question

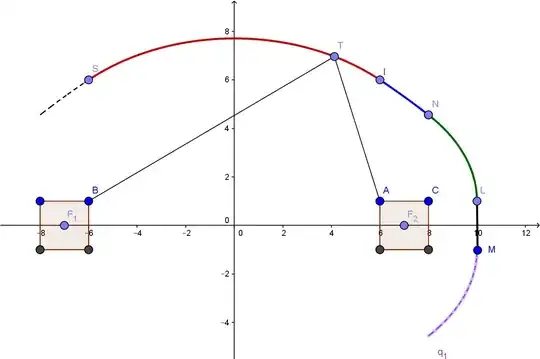
Consider the graphical representation below:

It describes a generalized ellipse $(E)$ in the following sense:

$$(E)=\{M \ \ | \ \ d(M,(S_1))+d(M,(S_2))=18 \}$$

where

• $(S_1)$ and $(S_2)$, playing a role of "generalized foci", are the squares centered in $F_1(-7,0)$ and $F_2(7,0)$ with sides' length 2,

• $d(M,(C))$ is the distance from a point $M$ to a convex set $(C)$ defined by $inf_{C \in (C)} d(M,C)$ where $d(.,.)$ is the usual (Euclidean) distance.

$d(M,(C))$ being a continuous function of $M$ (see for example (Distance to a closed set is continuous.)), generalized ellipse $(E)$ is piecewise continuous.

I would like to show that it is more than that: that it is smooth, in a geometrical sense: (what is called sometimes $\Delta^1$) in each connection point of two arcs (see below) there is a common tangent (as a consequence, it will be possible to define a $C^1$ parameterization).

Question: is there a simple mean to establish this "smoothness" ?

My work: I have established this smoothness explicitly by

• first computing the equations of the different constituent arcs of $(E)$.

• then for each connecting point (such as $L, N, I$...), by computing the left and right derivative (when it exists) and checking that their values are equal or checking the presence of a vertical tangent.

Due to $Ox$ and $Oy$ symmetries, it suffices to describe the first quadrant part of (E), or, in an equivalent form, the different parts of arc MLNIS. Here are the equations of the constituent arcs:

$$\begin{cases} \text{Arc ML:}\ &\text{line segment:} \ \ & x=10 & -1 \leq y \leq 1\\ \text{Arc LN:}\ &\text{ellipse with foci B and C:} \ \ & \frac{(x-1)^2}{81}+\frac{(y-1)^2}{32}=1& 8 \leq x \leq 10, 1 \leq y \leq \frac{41}{9}\\ \text{Arc NI:}\ &\text{parabola:} \ \ & y=- \frac{1}{36}(x+6)^2+10& 6 \leq x \leq 8, \frac{41}{9} \leq y \leq 6\\ \text{Arc IS:}\ &\text{ellipse with foci B and A:} \ \ & \frac{x^2}{81}+\frac{(y-1)^2}{45}=1& -6 \leq x \leq 6, 6 \leq y \leq 8 \end{cases}$$

But of course, it is very tedious... Moreover I would like to generalize this study to "generalized foci" that could be any polygonal shape, and even any convex curve.

Answer 1

Here's a conceptual sketch:

If $P$ is a convex polygon, the distance function $$ f_{P}(x) = d(x, P) $$ is of class $C^{1}$ outside of $P$: Each level set of $f_{P}$ is a union of finitely many line segments (each parallel to and of the same length as some side of $P$) and circle arcs (each centered at a vertex of $P$). Since an arc of a level set $\{f_{P} = c\}$ is tangent to any segment it meets (the sublevel set $\{f_{P} \leq r\}$ is the Minkowski sum of $P$ with a closed disk of radius $r$), each level curve is of class $C^{1}$. The gradient of $f_{P}$ is therefore continuous (as well as non-vanishing) outside $P$, proving that $f_{P}$ is continuously-differentiable.

Now suppose $(P_{i})_{i=1}^{n}$ is a finite collection of convex polygons. Let $f_{i} := f_{P_{i}}$ be the distance to $P_{i}$, and let $$ f = \sum_{i=1}^{n} f_{i} $$ be the sum of the corresponding distance functions. Since each $f_{i}$ is of class $C^{1}$ outside $P_{i}$, the function $f$ is of class $C^{1}$ outside the union of the $P_{i}$.

If $c$ is sufficiently large (e.g., if the level curve $\{f = c\}$ encloses all the $P_{i}$), then the level $\{f = c\}$ is of class $C^{1}$ by the implicit function theorem: The gradient of $f$ is a sum of non-vanishing gradient fields, and for a point sufficiently far from every $P_{i}$, the gradients of the $f_{i}$ lie in some closed half-plane, so their sum is non-zero.

Particularly, if $P_{1}$ and $P_{2}$ are your squares, the gradient of $f = f_{1} + f_{2}$ is non-vanishing on your "generalized ellipse" $E = \{f = 18\}$, so $E$ is of class $C^{1}$.