Let $a$ and $b$ be reals with $a<b$. Show that there are infinitely many rationals $x$ such that $a<x<b$.
My plan of action was to assume that $x$ is the smallest such rational and find another rational in the interval $(a, x)$, but I am struggling to make it work. A hint will be much preferred to a full solution.
Note that the real numbers are an Archimedean field, so for any real number $r$ we have some integer $n>r$. This means that for any real number $\epsilon>0$, we have some $n>1/\epsilon$, so $1/n<\epsilon$. Furthermore, the rationals are dense in the reals, so we can find some rational $x$ such that $a<x<b$.
Let $n$ be such that $1/n<b-x$. Then $x+\frac{1}{n},x+\frac{1}{n+1},\ldots$ is an infinite set of rationals between $a$ and $b$.
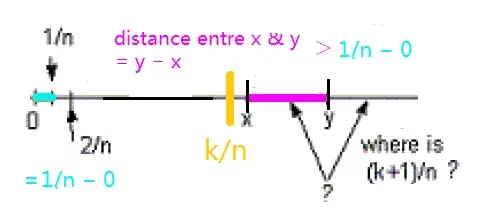
Maybe one can try something like this. Using the following
Lemma 1. For every real number $x$ there is exactly one integer $N$ such that $N \le x < N + 1$. (This integer $N$ is called the integer part of $x$, and is sometimes denoted $N = \lfloor x \rfloor$.)
Lemma 2. For any positive real number $x > 0$ there exists a positive integer $N$ such that $0 < 1/N < x$.
We now show
Proposition 3. Given any two real numbers $x < y$, we can find a rational number $q$ such that $x < q < y$.
By hypothesis, we have $y -x$ is positive. By Lemma 2, exists a positive integer $N$ such that $0 < 1/N < y - x$. Since $xN$ is a real number, by Lemma 1, there exists a integer $n$ such that $n - 1 \le xN < n$, i.e., $n/N - 1/N \le x$ and $x < n/N$. Thus $x < n/N \le x + 1/N$. Since $1/N \le y - x$, i.e., $x + 1/N < y$, we have $x < n/N < y$. Thus $n/N$ is rational, the claim follows.
If you already know (or can prove) that there is at least one rational between any two real numbers, then you can do this for $a < b$:
There is a rational number $x$ such that $a < x < \frac{a+b}{2}.$
There is a rational number $y$ such that $\frac{a+b}{2} < y < b.$
Now $a < x < y < b,$ with $x$ and $y$ rational.
There is no smallest such rational. But your basic strategy will work if we can show there is at least one such rational. We sketch a proof of the fact that there are at least two. There is some detail that needs to be filled in.
Let $\epsilon=\dfrac{1}{b-a}$. Then by something that has undoubtedly already been proved, there is a positive integer $N$ such that $\dfrac{1}{N}\lt \epsilon/2$.
There is a largest integer $m$ such that $\dfrac{m}{N}\lt a$. Argue that $$a\lt \frac{m+1}{N}\lt \frac{m+2}{N}\lt b.$$
This PDF may help, but I improved the picture :
Whence we observe by inspection : $\color{#1FB4BF}{1/n} < \color{#E431D2}{(y - x)}$ for all $x, y \in \mathbb{R}$.
Separately from the line above, we also know $ \; k/n < x $.
Add both inequalities above: $ k/n + \color{#1FB4BF}{1/n}< x + \color{#E431D2}{(y - x)}$.
In summary, $k/n + \color{#1FB4BF}{1/n} = \dfrac{k+1}{n}$ $\in (x,y)$ is the rational number desired.
Say $a\ne b$ and we want to show that infinitely many rationals are between $a$ and $b$. Then $|a-b|>0$. Is there an integer $n$ so big that $1/n < |a-b|$? If not, then $|a-b|>0$ is a lower bound of the set $\{1/n:n\in\{1,2,3,\ldots\}\}$, which therefore has an infimum $c$ that is positive and therefore has a reciprocal $1/c>0$, and $c=\sup\{1,2,3,\ldots\}$. Since $c>0$ is the smallest number greater than every positive integer, $c/2$ is smaller than sum positive integer $n$, so $c$ is smaller than $2n$, but $2n$ is a positive integer, so we have a contradiction. Conclusion: for some positive integer $n$, we have $1/n<|a-b|$. From there it's not hard to show that for every denominator $m\ge n$, some rationals with denominator $m$ are between $a$ and $b$.
