I kind of stumbled across this pattern recently and cant make any sense of it. Attached is my work explaining what I did. If there is already an answer to this please post the link. Thanks!
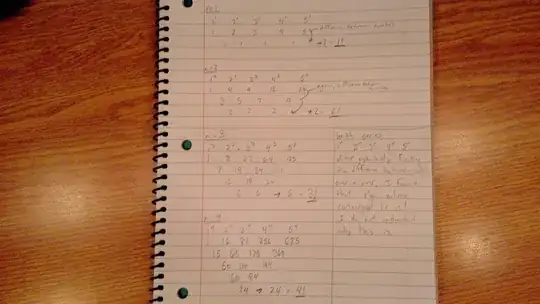
I kind of stumbled across this pattern recently and cant make any sense of it. Attached is my work explaining what I did. If there is already an answer to this please post the link. Thanks!
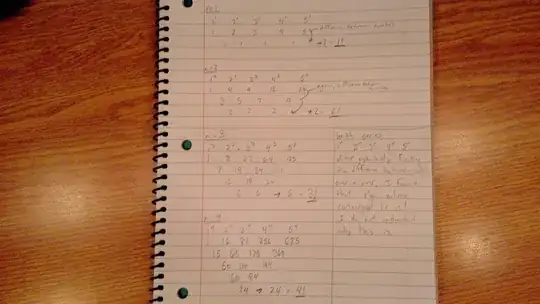
Hint. If you form a row $$p(1)\quad p(2)\quad p(3)\quad\cdots$$ from any polynomial $$p(x)=ax^n+\cdots\ ,$$ then the next row will be $$q(1)\quad q(2)\quad q(3)\quad\cdots$$ where $$q(x)=nax^{n-1}+\cdots\ .$$
It's more natural to start the sequence at $0$: for example,
$$0 \quad 1 \quad 4 \quad 9$$ $$1 \quad 3 \quad 5$$ $$2 \quad 2$$ $$0$$
from which you can read off the leftmost side that the top (the sequence $n^2$, $n \in \mathbb{N}$) is actually $$\color{red}{0} \cdot \binom{n}{0} + \color{red}{1} \cdot \binom{n}{1} + \color{red}{2} \cdot \binom{n}{2} = n + 2 \cdot \frac{n(n-1)}{2}.$$
This idea goes by the name Binomial transform.
The fact that you will end up with the last coefficient $k!$ when studying the sequence $1^k,2^k,3^k$ is because the coefficient of $n^k$ in $\binom{n}{k}$ itself is exactly $1/k!$; and you need the result to be $1 \cdot n^k.$