0

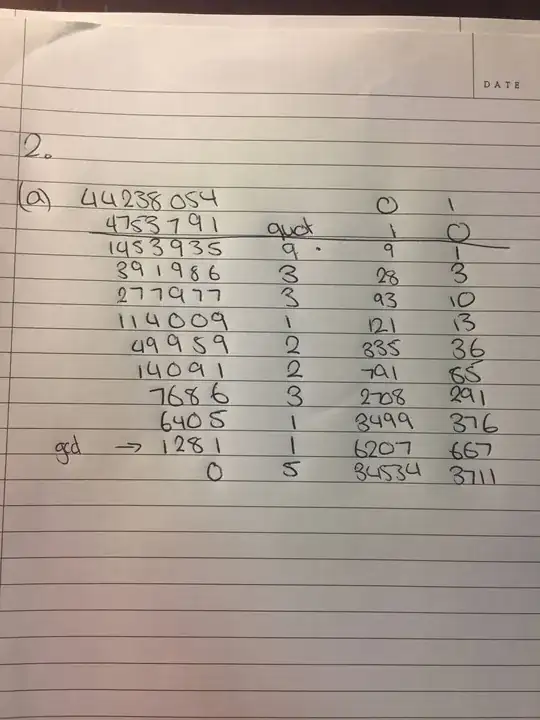
Hi so I am doing this question trying to find the greatest common factor of $a = 44,238,054$ and $b = 4,753,791$ and this is what I got but I don't think it is right. Was hoping someone could tell me what I've done wrong, thank you. :)

enter image description here

the rest of the question is:

b) find integers $x$ and $y$ so that $g = 44,238,054x + 4,753,791y$.

c) check whether 167,811 is a multiple of $g$ (it should be) find integers $s$ and $t$ such that $167,811 = 44,238,054s + 4, 753,791t$. Don't just give a single $r$ and $s$, but find all pairs of integers $(r,s)$ that satisfy this equation.

d) As part of your answer to part (c) you should check that the numbers you have found do indeed satisfy the given equation any difficulties you encountered while doing such a check, and how you overcame them.

If anyone could explain these questions and what working I'm supposed to do it would be really appreciated thank you :)

George Law
  • 4,103
Marissak
  • 55

2 Answers2

1

As explained in my comment the HCF for(444238054,4753791) is 1281. For the answers to parts b and c we follow the steps to find the solutions to linear Diophantine equations the procedure of which is given in the following link:How to find solutions of linear Diophantine ax + by = c?

Community
  • 1
1

You didn't have alternating signs. You should have found in the last but one row: $\color{red}{-}6207, 667$. That said you have the coefficients of a Bézout's relation between $44,238,054$ and $4,753,791$ and you can write $$1281=-6207\times4{,}753{,}791+667\times44{,}238{,}054.$$ You can check $167,811=331\times1281=331(-6207\times4{,}753{,}791+667\times44{,}238{,}054)$, whence a solution of the equation $44{,}238{,}054\,x+4{,}753{,}791\,y$: $$(x_0,y_0)=(331\times667,-331\times 6207)=(220{,}777\,; 2,054{,}517)$$ The general solution is given by \begin{align}x&=x_0+k\frac{4,753,791}{1281}=220{,}777+3711k, \\ y&=y_0-k\frac{44{,}238{,}054}{1281}=2,054{,}517-34{,}534k\qquad(k\in\mathbf Z) \end{align}

Bernard
  • 175,478