2

The resolution of the cubic equation is known to have a "casus irreductibilis" such that the computation of real roots requires an excursion in the complex numbers. The usual formulas involve trigonometric functions and essentially amount to the evaluation of

$$\cos\left(\frac{\arccos x+2k\pi}3\right)$$ which solves the angle trisection problem.

I would like to know if other formulations are known, which might be more computationally efficient.

The hyperbolic counterpart is

$$\cosh\left(\frac{\text{argcosh }x}3\right)=\cosh\left(\frac{\log\left(x+\sqrt{x^2-1}\right)}3\right)=\frac12\left(\sqrt[3]{x+\sqrt{x^2-1}}+\sqrt[3]{x-\sqrt{x^2-1}}\right).$$

Update:

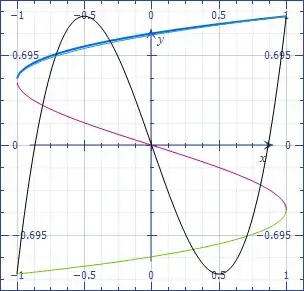
By simple trigonometry, the function is in fact the three-branched inverse of the cubic $4x^3-3x$.

If a good approximate solution can be estimated, maybe a few Newton's iterations can quickly polish. The blue branch is close to

$$\sqrt{\dfrac{x+1}8}+\frac12.$$

enter image description here

  • yves, there is a distinction between the version you mention, with an arccos, and some cleaner versions which are sums of roots of unity, so that it becomes a sum of a small number of $2 \cos ( 2 \pi / k).$ Recently two kids asked about $x^3 + x^2 - 10 x - 8$ I think, let me find those; I made various comments on or related to those, so you could just look under my "all activity" under comments. – Will Jagy Oct 27 '16 at 19:22
  • http://math.stackexchange.com/questions/1065862/something-strange-about-sqrt-4-sqrt-4-sqrt-4-x-x-and-its-friends#comment4072546_1065862 – Will Jagy Oct 27 '16 at 19:24
  • answer by Tito http://math.stackexchange.com/questions/1980175/how-would-you-find-the-trigonometric-roots-of-a-cubic/1983746#1983746 – Will Jagy Oct 27 '16 at 19:33
  • answer by mercio http://math.stackexchange.com/questions/1980693/finding-the-roots-of-any-cubic-with-trigonometric-roots/1982039#1982039 – Will Jagy Oct 27 '16 at 19:35
  • @WillJagy Is there a general formula for $x\in\mathbb R$ ? –  Oct 27 '16 at 19:38
  • emphasize one point, in $x^2 + a x^2 + b x + c$ we may take an integer translation to alter $a$ by any multiple of $3.$ So, the cases can be $x^3 + x^2 + b x + c,$ then $x^3 + bx + c,$ then $x^3 - x^2 + bx + c.$ No important difference between first and third. Easy enough to compute a list with $|b|, |c| < 1000$ and the discriminant of $x^3 + x^2 + b x + c$ a square, which is how the Galois group becomes cyclic $\mathbb Z_3$ – Will Jagy Oct 27 '16 at 19:39
  • What for $\cos \left( (1/3) \arccos x \right)?$ I don't know. – Will Jagy Oct 27 '16 at 19:40
  • @WillJagy: this is what my question is about (I tagged numerical methods). –  Oct 27 '16 at 19:41
  • I see. Well, proper I just left comments, then. – Will Jagy Oct 27 '16 at 19:42
  • I am puzzled about the proper spelling, which was edited from irreductibilis to irreducibilis. If I am right, the adjective derives from reducere, reductum. The spelling irreduciblilis smells an English influence. –  Oct 27 '16 at 21:10
  • I've never seen it with a "t." You may have a point, though, Wantzel wrote irreductible http://archive.numdam.org/ARCHIVE/NAM/NAM_1843_1_2_/NAM_1843_1_2__117_1/NAM_1843_1_2__117_1.pdf Wonder what Cardano wrote, or Ruffini – Will Jagy Oct 27 '16 at 21:36
  • @WillJagy: this is in French. The latin word is irreductibilis. https://books.google.be/books?id=buM2AAAAMAAJ&pg=PA242&dq=casus+irreductibilis&hl=fr&sa=X&ved=0ahUKEwjC9sOZ_vvPAhVSahoKHZjzAWsQ6AEIVDAH#v=onepage&q=casus%20irreductibilis&f=false –  Oct 27 '16 at 22:00
  • I see what you mean..by the time of Wantzel it had found its way into French with a "t," probably into other languages without a "t." Similar story to how the Gamma function is shifted one from the factorial. http://mathoverflow.net/questions/20960/why-is-the-gamma-function-shifted-from-the-factorial-by-1/20962#20962 – Will Jagy Oct 27 '16 at 22:17
  • 1
    @WillJagy: from a little Web search, I see both spellings in Italian or German texts, and always without the 't' in English references. –  Oct 27 '16 at 22:34

0 Answers0