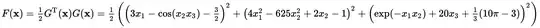I was reading the Wikipedia page for gradient descent, but I don't understand how the objective function:
Can be used to solve for $x_1, x_2,x_3$ as the objective function seems a bit arbitrary and I don't see how minimizing it will give the solution to the system of non-linear equations. Is there something that I am missing?
In the example given, the nonlinear system of equations is: $$ \begin{cases} 3x_1 - \cos(x_2x_3) - 3/2 = 0\\ 4x_1^2 - 625x^2_2 + 2x_2 - 1 = 0\\ \exp(-x_1x_2)+20x_3+(10\pi-3)/3 = 0 \end{cases} $$ Then $G$ is defined: $$ G(\vec{x})=\begin{bmatrix} 3x_1 - \cos(x_2x_3) - 3/2 \\ 4x_1^2 - 625x^2_2 + 2x_2 - 1 \\ \exp(-x_1x_2)+20x_3+(10\pi-3)/3 \end{bmatrix}= \begin{bmatrix} g_1(\vec{x}) \\ g_2(\vec{x}) \\ g_3(\vec{x}) \end{bmatrix} $$ which is a vector in $\mathbb{R}^3$.
Note that the equation is solved when $G=0$. So the idea is to minimize $G$ as much as possible (i.e. make it close to $0$). The most logical way to do that is to simply minimize the norm of $G$ (i.e. $||G||$). So we define: $$ F(\vec{x})= \frac{1}{2} ||G(\vec{x})||_2^2 = \frac{1}{2}G^T(\vec{x})G(\vec{x}) = \frac{1}{2}\left( g_1^2(\vec{x})+g_2^2(\vec{x})+g_3^2(\vec{x}) \right) $$ where we square the norm because the transformation preserves ordering, so there is no need for the extra computational cost of the square root. Also, constant coefficients don't matter in the objective function, so we multiply by $1/2$ for mathematical "niceness" (it will cancel the $2$s that come from differentiating $F$ to compute $\nabla F$, which has squares).
