When $\delta$ decreases should $\epsilon$ decrease? (In the definition of a limit when x approaches $a$ should $f(x)$ approach its limit $L$? )

Question

Assume that the function $f$ has the following limit:

$$\lim_{x \rightarrow a} f(x) = c$$

if I have the correct understanding of what this definition should mean, the following should be true:

$$ \text{if } |x - a| \rightarrow 0 \implies | f(x) - c | \rightarrow 0$$

if this understanding is correct then using the delta-epsilon definition of a limit (as a reference here is the definition $ \forall \epsilon>0 , \exists \delta > 0, if |x -a| < \delta \implies |f(x) - c| < \epsilon $ ) then the following should be true:

if we get $x$ closer to $a$ then we should get $f(x)$ closer to $c$. i.e. $ \delta_1 < \delta_2 \implies \epsilon_1 < \epsilon_2$ in other words when getting closer by shifting to $\delta_1$ then we should get closer by some other $\epsilon_1$. In other words, if $\delta$ decreases so should $\epsilon$ (probably not visa versa since the converse of the implication of a limit means something different).

My intuition is totally convinced this should be true so I proceeded to find a proof (that I assumed was a standard real analysis exercise).

So I started by choosing two different $\epsilon_1$ and $\epsilon_2$, so $\epsilon_1 \neq \epsilon_2 $ (I started here because its first thing to fix in the quantifiers in the definition of a limit). Then by the definition of a limit they both have their own $\delta$'s call them $\delta_1, \delta_2 > 0$. It seemed reasonable to assume $\delta_1 \neq \delta_2$ because otherwise it seems that $f(x)$ wouldn't be a function (i.e. it could have one single $x$ that maps two different values of $f(x)$ in particular the values of $f(x) = c \pm \epsilon_1, c \pm \epsilon_2$ would have the same corresponding $x$ value $x = a \pm \delta_1 = a \pm \delta_2$ ). Hopefully that assumption is right. So WLOG assume $\delta_1 < \delta_2$ since the real numbers have a strict ordering. Now what I hope to show is that $\epsilon_1 < \epsilon_2$ (with not success yet). This gave me two starting facts to start the proof:

1. if $ | x -a | < \delta_1 \implies | f(x) - c | < \epsilon_1$
2. if $ | x -a | < \delta_2 \implies | f(x) - c | < \epsilon_2$

we know also know that:

3. $ | x -a | < \delta_1 < \delta_2 \implies | f(x) - c | < \epsilon_2 $

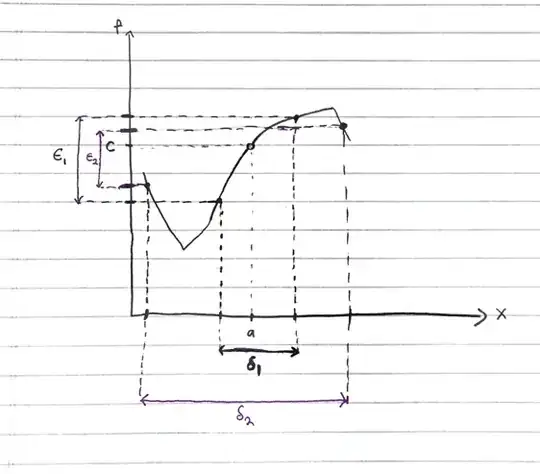
which seemed enough to start the proof. However, as I tried to proceed I got really stuck because I thought I found a counter example to the proof I am trying to do. Let me share you the picture which I think is the counter example (which I hope is wrong somewhere):

which shows the opposite of what I expected to have. When I move from $\delta_1$ to $\delta_2$ I actually get a increase in $\epsilon$. i.e. $\epsilon_2$ is in fact smaller than $\epsilon_1$, which is opposite of what my intuition tells me. I don't know if I actually have to maybe make a further assumption in $f(x)$ to make it work (I thought maybe I needed to assume continuity but the function I drew can easily be made continuous without hurting my argument I believe). In fact as we increase $\delta$ it seems at least in this example that we can have $f(x)$ approach $c$. I am not sure what is the fault in my argument/thinking but the two things I would appreciate most in the answer are:

1. Explaining why my counter argument is wrong (which I believe it is)
2. providing some hints on how to actually proceed to a correct proof
3. if possible even the actual proof of the statement that I am looking for (maybe the answer can be hidden so that I can give it a try first with the hints? but it would drive me crazy not to know for sure correct proof because I've embarrassingly been stuck on this for a week or two with this)

Answer 1

When $\lim_{x\to a} f(x) = c$, it isn't just a matter that every time you "move" $x$ closer to $a$, $f(x)$ gets closer to $c$. In fact it very often will be that sometimes while you are moving $x$ closer to $a$, $f(x)$ will get farther from $c$, as your example demonstrated. Your example appears indeed to be a counterexample to the kind of proof you were working toward, because it appears your method of proof is incorrect.

The flaw in the proof may be due to your definition of a limit, which appears to be missing a couple of important parts. Here is a more complete definition with the parts you are missing shown in red: $$ \forall \epsilon>0 \; \exists \delta > 0 \;\color{red}{\forall x}\; (\color{red}{0 <}\lvert x -a \rvert < \delta \implies \lvert f(x) - c \rvert < \epsilon ) $$

Note that some authors write something like $\forall x \neq a$ and leave out the "$0<$", some may not actually write $\forall x$ (but that quantification over $x$ is supposed to be understood implicitly), and some write neither $x\neq a$ nor $0<\lvert x - a\rvert$ (possibly because those facts also are supposed to be understood implicitly; there was another question recently asked about that).

By the way, there is a technical error in the way you constructed your counterexample that does not invalidate the counterexample but may indicate a misunderstanding of the the meanings of $\lvert x -a \rvert < \delta$ and $\lvert f(x) - c \rvert < \epsilon$, namely, $\lvert x -a \rvert < \delta$ is equivalent to $a - \delta < x < a + \delta$: graphically, to represent $\lvert x -a \rvert < \delta$ you should indicate an interval along the $x$-axis that extends an equal distance $\delta$ to both the left and right sides of $a$. That is, the interval is symmetric around $a$ and the total width of the interval is $2\delta$. Similarly, $\lvert f(x) - c \rvert < \epsilon$ is represented by an interval on the $y$-axis that is symmetric around $c$ and whose total height is $2\epsilon$.

Keeping the correct interpretation of $\lvert x -a \rvert < \delta$ in mind, we can still see from your counterexample that sometimes, for a larger $\delta$, the function values at the extreme ends of the $x$ interval, $f(a - \delta)$ and $f(a + \delta)$, may be closer to $c$ than they would be for a smaller $\delta$. But you cannot simply measure $\lvert f(a - \delta) - c \rvert$ or $\lvert f(a + \delta) - c \rvert$ and say that's your value of $\epsilon$. There are several errors in that idea:

1. The two values $\lvert f(a - \delta) - c \rvert$ and $\lvert f(a + \delta) - c \rvert$ may not be equal.
2. There may be values of $x$ between $a - \delta$ and $a + \delta$ for which $\lvert f(x) - c \rvert$ is much larger than either $\lvert f(a - \delta) - c \rvert$ or $\lvert f(a + \delta) - c \rvert$.
3. The whole idea of deriving $\epsilon$ from $\delta$ is backwards: you need to have a rule such that someone can give you any value of $\epsilon$ and then you can use the rule to give them back a suitable value of $\delta$. In short, we get $\epsilon$ first, and then we find $\delta$.

The last point is really the important one. The definition of the limit does not make $\epsilon$ depend on $\delta$ in any way; in fact it's the other way around.

It's OK to have an intuition that restricting $x$ to a tighter interval around $a$ will constrain $f(x)$ to be within a tighter interval around $c$, because this is true, as long as you remember that the interval that $f(x)$ is constrained to is not just the interval that contains $f(a-\delta)$ and $f(a+\delta)$; it must also contain all the values of $f(x)$ in all the peaks and valleys that occur for $x$ between $a-\delta$ and $a+\delta$. This intuition doesn't really help construct a proof, however, because it's not how the definition of a limit is structured.

To make a correct standard analysis proof of a limit using the $\delta$-$\epsilon$ definition directly, you start with the premise that a value of $\epsilon$ has somehow been decided, and then (without relying on any assumptions about what value of $\epsilon$ might have been chosen) show how to set $\delta$ to a value such that $$ \forall \epsilon>0 \; \exists \delta > 0 \;\forall x\; (0 < \lvert x -a \rvert < \delta \implies \lvert f(x) - c \rvert < \epsilon ). $$ While doing this, it often helps to keep in mind that there is no such thing as a positive $\delta$ that is too small. Choosing a smaller $\delta$ is always OK, because that never puts new values of $f(x)$ into the set of $f(x)$ values that have to fit inside the interval $(c - \epsilon, c + \epsilon)$.

---

Update:

In light of further comments, it seems there is a more fundamental misconception here.

Although we often speak of functions as one-directional things that go from elements of a domain to elements of a co-domain, in fact a function is just a relationship between the elements of the domain and co-domain. The thing that makes it a function is just that each element of the domain participates in this relationship exactly once: the function relates one (and only one) element of the co-domain to each element of the domain. It is absolutely not necessary that every time we speak of a function we must "start" in the domain and "finish" in the co-domain.

If you would like to think of a function as drawing little "arrows" that start in the domain and end in the co-domain, and think of the function as "going from" the tail of an arrow to its head, fine. None of that should stop you from looking at a ball in the co-domain and asking, "Hey, what arrows point into here, and can I find a ball in the domain that is covered completely by their tails?"

It seems that your first mistake may be the idea that the "direction" of a function conflicts with the right to ask such a question.

Answer 2

In the title I read: "If $\delta$ decreases, should $\epsilon$ decrease?". Of course, if $\delta$ decreases, the quantity $$\omega(\delta):=\sup_{0<|x-a|<\delta}\bigl|f(x)-c\bigr|$$ decreases as well, for purely logical reasons. But the issue at stake is the following: The devil has set a tolerance $\epsilon>0$, and the question is: Will $\omega(\delta)$ decrease in fact to $0$, so that at some point $\omega(\delta_\epsilon)<\epsilon$? The exact point $\delta_\epsilon$ where this happens is of no importance; we just want to be sure that such a $\delta_\epsilon$ exists, however small the tolerance $\epsilon>0$ the devil has set.

Answer 3

Notice in choosing $\delta_i$ you chose the largest possible deltas you could. In that case there is no reason at all that $\delta_2 < \delta_1$. That simply is not a requirement. Indeed on any continuous not injective function this will always be possible.

=====

Intuitively, but incorrectly, it seems as though the definition of limit should be (but it isn't), that "as $x$ gets closer to $a$ then $f(x)$ gets closer to $c$". I think it is this intuitive, but incorrect, concept that is throwing you off.

The problem with this definition is it really isn't very meaningful. How do you measure "closeness"? What if the function bounces all over the place, gets close to $c$ but then really far away from $c$ and only in one little micron close to $a$ does the function actually "calm down" and "go to c"? What if the function gets very close to $c$ and then gets far from $c$ and then close to $c$ again as $x$ gets close to $a$. (This is pretty much the behavior you are describing.)

And what if the function "hits" $c$ early and simply stays there?

So the actual definition is to find the "closeness" that $f(x)$ gets to $c$ (i.e. $\epsilon$) determines that there is a closeness of $x$ to $a$ (i.e. $\delta$) that assures this. BUT that $\delta$ need need not be unique, and, subtly$ those $\delta$ need not be getting any smaller.

Consider $f(x) = c$ and $\lim+{x\rightarrow a}(x) = c$. Let $\epsilon = .1$ and let $\delta = 5,000,000,000$ then $|x - a| < 5,000,000,000 \implies |f(x) -c|< .1$. Now let $\epsilon_2 = .000000000000001$ and $\delta_2 = \infty$ then $|x - a| < \infty \implies |f(x)-c|< \epsilon_2$.

Now one might argue why choose a large delta when a small delta will be better. Or more sophisticated if $\epsilon_2 < \epsilon_1$ and $\delta_2 \ge \delta_1$ why couldn't we have used $delta_2$ instead of $\delta_1$ in first place. i.e $|x - a| < \delta_2 < \delta_1 \implies |f(x)-c| < \epsilon_1$. And yes, we could have.

But we didn't have to.

$\epsilon_3 < \epsilon_2 < \epsilon_1$ does NOT mean $\delta_3 < \delta_2 < \delta_2$. However we can state $\min(\delta_3,\delta_2,\delta_1) \le \min(\delta_2, \delta_1) \le \delta_1$. (Which... come to think of it is always true so it's pointless to point it out.)

In your exampe for $\epsilon_2$ you chose the largest $\delta_2$ you could. SO you ended up with $\delta_2 > \delta_1$. And.... that's not a contradiction. Instead of picking the large $\delta_2$ you could have picked something much smaller. You could have picked $\delta_1$ because if you look at you diagram if $|x - a| < \delta_1$ then $|f(x) - c| < \epsilon_2$ (just look at you picture-- it is true the way you drew it.) You could even have draw a $delta_3 < \delta_1$.

Instead of picking the largest deltas, try picking smaller deltas.

Answer 4

It is true that $\lim_{x\to a}f(x)=c$ means that there exists some function $\delta=\delta(\varepsilon)$ mapping every $\varepsilon>0$ to $\delta(\varepsilon)>0$ s.t. $|x-a|<\delta \Rightarrow |f(x)-c|<\varepsilon$. However, note that any function $\tilde{\delta}$ such that $0<\tilde{\delta}(\varepsilon)<\delta(\varepsilon)$, for every $\varepsilon>0$, also has the above property. Hence a function $\delta(\cdot)$ is not uniquely defined and may not be monotonic. In other words, while smaller values of $\varepsilon$ typically correspond to smaller values of $\delta$ for ''reasonable'' choices of $\delta(\cdot)$ (i.e. in cases when $\delta(\cdot)$ is chosen to be strictly increasing), it is not necessarily true in general.

As an example, consider $f(x)=x$, $a=0$ (or any other number) and pick \begin{align} \delta(\varepsilon)= \begin{cases} \varepsilon, \quad \text{for } 0<\varepsilon<1,\\ 1, \quad \text{for } 1\leq \varepsilon<2 \\ \varepsilon-1, \quad \text{for } \varepsilon\geq 2. \end{cases} \end{align} It can be easily verified that such $\delta(\cdot)$ is a valid choice, although it is not strictly increasing and hence smaller values of $\varepsilon$ do not necessarily correspond to smaller values of $\delta$ (consider $\varepsilon_1=1,\varepsilon_2=2$).

Answer 5

I think the main mistake of my question has been clearly pointed out that I was looking at just the edges approaching the limit rather than looking at everything within $\delta$ of the limit point $p$ to not jump by more than $\epsilon$. Thanks!

But I think I found the concept I was truly looking for which is the following:

For a given $\epsilon$ show that the largest $\delta^*_{\epsilon}$ decrease whenever $\epsilon$ decreases. So

Theorem: if $\epsilon_2 < \epsilon_1 \implies \delta^*_{\epsilon_2} \leq \delta^*_{\epsilon_1}$ for any limit in consideration $\lim_{x \rightarrow p} f(x) = q$.

Sketch proof:

Points within $\delta^*_{\epsilon_1}$ of $p$ satisfy being $\epsilon_1$ from the limit $q$. But there are points between $\epsilon_1$ and $\epsilon_2$ that are considered by $\delta^*_{\epsilon_1}$ but that don't necessarily satisfy $\delta^*_{\epsilon_2}$ since $\delta^*_{\epsilon_2}$ only needs points to be bellow $\epsilon_2$ (but there are points $x$ within $\delta^*_{\epsilon_1}$ that are too large since they lead to an $\epsilon_1$ jump). In other words the tighter $\epsilon_2$ leads to points with a tighter $\delta^*_2$. Therefore, the largest radius ball $\delta^*_{\epsilon}$ must decease as $\epsilon$.

Formal proof:

Let $\epsilon_2 < \epsilon_1$. Let the set of all deltas that work for a given $\epsilon_i$ to be defined as follows:

$$ D_{\epsilon_i} = \{ \delta \in R \mid \forall x \in E, 0< d(x,p) < \delta \implies d(f(x),q) < \epsilon_i \} $$

now define the largest radiuses that are within their corresponding tolerance $\epsilon_i$ as follows:

$$ \delta^*_{\epsilon_1} = \sup D_{\epsilon_1} $$ $$ \delta^*_{\epsilon_2} = \sup D_{\epsilon_2} $$

notice that for $ \delta^*_{\epsilon_2} $ (corresponding to the tighter tolerance level) we have the following condition (notice the last inequality):

$$ D_{\epsilon_1} = \sup \{ \delta \in R \mid \forall x \in E, 0< d(x,p) < \delta \implies d(f(x),q) < \epsilon_2 < \epsilon_1 \} $$

the tighter inequality implies that the set of points that satisfy that must be smaller and thus also the $\delta$ must be smaller since, if $\delta_{\epsilon_2} \in D_{\epsilon_2}$ then it must mean that $\forall x \in E, 0 < |x - p| < \delta_{\epsilon_2} \implies |f(x) - L| < \epsilon_2$ but since this same delta $\delta_{\epsilon_2}$ satisfies $\forall x \in E, 0 < |x - p| < \delta_{\epsilon_2} \implies |f(x) - L| < \epsilon_2 < \epsilon_1$ then it must mean that $\delta_{\epsilon_1} \in D_{\epsilon_1}$.

So we have:

$$ D_{\epsilon_1} \subseteq D_{\epsilon_2} $$

since $ D_{\epsilon_1} $ contains all points of $ D_{\epsilon_2} $ or less, it cannot introduce a larger number by accident. Therefore we have the following holds for their supremums then:

$$ \sup D_{\epsilon_1} \leq \sup D_{\epsilon_2} $$

which is equivalent to:

$$ \delta^*_{\epsilon_1} \leq \delta^*_{\epsilon_2} $$

as required.

---

Note that its crucial to talk about largest $\delta$ because with the standard definition of $\epsilon-\delta$, using some $\delta_2$ such that $\delta_2 < \delta_1$ "works" for satisfying being within $\epsilon_1$ and $\epsilon_2$, since we have:

$$ x \in E, 0 < |x - p| < \delta_2 \implies |f(x) - q| < \epsilon_2 < \epsilon_1$$

so one could use $\delta_2$ for the $\delta_1$ for $\epsilon_1$. It works but its not the largest as required by the question/theorem I required.

Perhaps this is obvious but I will point it out. If we have an $ \epsilon_1 > \epsilon_2$ then the $\delta_1$ might not work for the smaller $\epsilon$ (i.e. $\epsilon_2$). This is because if the larger $\delta$ is too larger then it might be that it contain points that are out of the $\epsilon_2$ bound but still smaller than $\epsilon_1$.