How to check differentiablity of the function $\min\{|x-2|,|x|,|x+2|\}?$ I only know that inside functions are not differentiable at $2,0,-2$ resp. Please help. Thanks a lot.
Asked
Active
Viewed 75 times
2
-
Take a look at this question – polfosol Oct 22 '16 at 07:30
-
1Draw its graph. – Did Oct 22 '16 at 07:31
-
i want mathematically solution... – neelkanth Oct 22 '16 at 07:32
-
Use the axioms of an ordered field to check where is $\min$ in each case for any partition of $\Bbb R$. – Masacroso Oct 22 '16 at 07:33
-
Me: "Draw its graph." OP: "i want mathematically solution..." Sure, we got that, but why should this fact prevent you from drawing a graph of the function? If you had followed my suggestion, the solution would have become obvious and you could have transformed what you would have seen on the graph into a full mathematical proof. Next time, you might want to try to understand suggestions before discarding them... – Did Oct 22 '16 at 07:52
-
1@Macroso Don't you think that "the axioms of an ordered field" is at 30000 feet above the mathematical level of neelkanth who is due to be ending his high school ? – Jean Marie Oct 22 '16 at 08:37
-
1This is very similar function to the one given in this famous answer. – Martin Sleziak Oct 22 '16 at 10:23
3 Answers
3
Hint: Graph it! Here is the piecewise of this function
$$ f(x) = \begin{cases} -2 -x, \; \; \; x<-2 \\ |x|, \; \; \; -2 \geq x \leq 2 \\ x -2 \; \; \; x > 2 \end{cases} $$
It looks something like this:
\ \/ /
ILoveMath
- 10,694
-
-
1I am sorry: there are not 3 cases, but 5 cases (see the graphical representation in my answer). – Jean Marie Oct 22 '16 at 07:38
-
1I thin you made a mistake, there are changes at -1 and 1 too (you have to split the [-2,2] domain. It looks more like /// – Edouard L. Oct 22 '16 at 07:38
-
Following your style ILoveMath the graph seems to be something like
\/\/\/– Masacroso Oct 22 '16 at 07:42 -
-
@Takahiro Waki I wouldn't like to be too insistant but the answer of ILoveMath is erroneous, and he/she should correct it. – Jean Marie Oct 22 '16 at 08:40
3
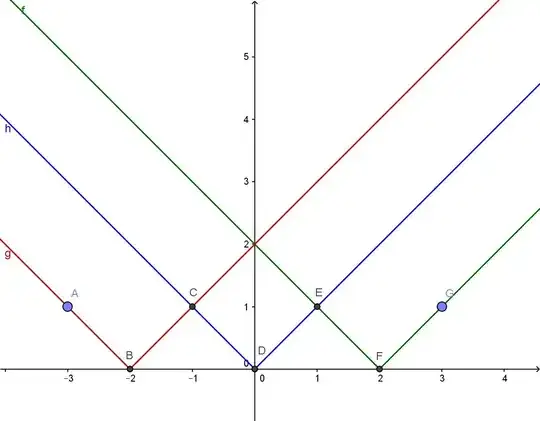
Hint: What is the connection between the broken line ABCDEFG and your problem?
What do you think for example in point B of the left derivative versus the right derivative?
Jean Marie
- 81,803
1
You can rewrite the function as follows:
1) On $]-\infty,-2], f(x)=f_1(x)=-x-2$
2) On $[-2,-1], f(x)=f_2(x)=x+2$
3) On $[-1,0], f(x)=f_3(x)=-x$
4) On $[0,1], f(x)=f_4(x)=x$
5) On $[1,2], f(x)=f_5(x)=-x+2$
6) On $[2,\infty[, f(x)=f_6(x)=x-2$
On each of the open domains, the function is linear and therefore differentiable.
At each of the "intermediate points" {-2,-1,0,1,2} the function is not differentiable (left and right limit of the derivative are different). For example, $f'_1(x)=-1$ and $f'_2(x)$=1, so that $\lim_{x \to -2^-} f'(x)=-1 \neq \lim_{x \to -2^+} f'(x)=1$
Edouard L.
- 581