3

How would one find all real solutions to the following equation:

$\qquad$ $n^n = 2^{2^{2^{2^{\dots^2}}}} $(where the number of $2$s is equal to $n$)

generalizing to $n$ being a real value. In tetration-notation this is

$\qquad $ find a solution to $\displaystyle \;^2 n = \; ^n 2$ for real $n \ne 2$.

I know one solution is $n = 2$, but I wonder if any other solutions exist.

Edit: Could there be any negative number solutions to this equation?

Svend Tveskæg
  • 83
Oawkem Jenster
  • 135
  • 2
    There is no standard meaning of tetration for non-integer values, as far as I know, so it is meaningless to talk of a solution "between" 3 and 4. – Dustan Levenstein Oct 17 '16 at 18:36
  • 1
    Just as it would be meaningless to have a "negative number of 2's" – JMoravitz Oct 17 '16 at 18:37
  • 1
    Well, this can get really abstract. For example, it might not make sense to exponentiate by a negative number of 2s, but think about n^-1 for example. It doesn't really make any sense at first, but we write it as 1/n instead to evaluate it. – Oawkem Jenster Oct 17 '16 at 18:39
  • 1
    @OawkemJenster Yes, but while there is a standard definition for exponentiation of more general numbers, the same is not true of tetration. Even exponentiation runs into problems after a while - if you're considering general complex numbers $z, w$ for exponentiation, then $z^w$ can have any finite or countably infinite number of valid values. – Dustan Levenstein Oct 17 '16 at 19:34

2 Answers2

3

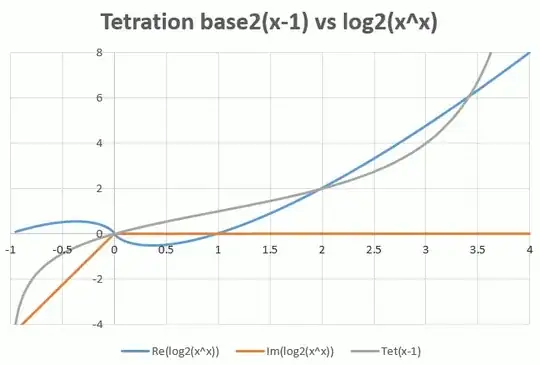
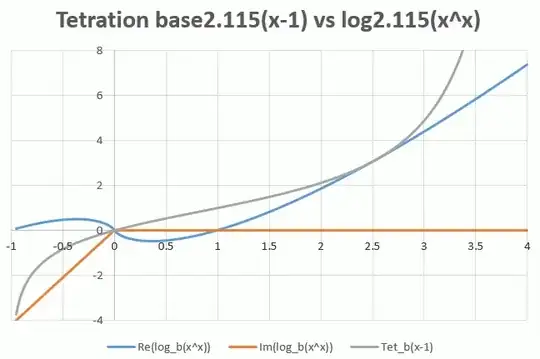
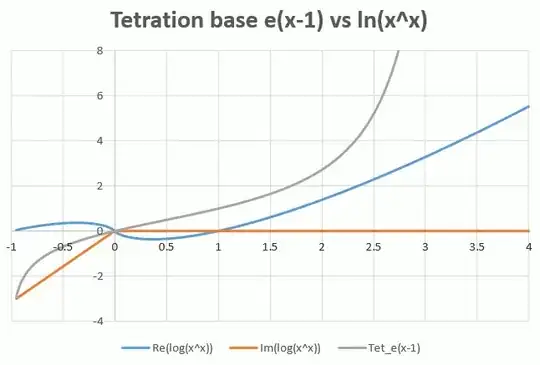
With a simple method, using the eigendecomposition of the $\small 16 \times 16, 24 \times 24,32 \times 32,48 \times 48,64 \times 64$ - sized truncated Carlemanmatrix for $f(x)=2^x$ , I get

 print(n)
 %191 = 3.41417132461  \\ for size 16x16
 %199 = 3.41417539283  \\ for size 24x24
 %206 = 3.41417594201  \\ for size 32x32
 %333 = 3.41417608600  \\ for size 48x48
 %387 = 3.41417609800  \\ for size 64x64  
 print(n-sqrt(2))
 %192 = 1.99995776224  \\ for size 16x16
 %200 = 1.99996183046  \\ for size 24x24
 %207 = 1.99996237964  \\ for size 32x32
 %388 = 1.99996253563  \\ for size 64x64

Possibly this indicates that $n=2+\sqrt {2}$ would be the extrapolated approximation when size of the matrix increases to infinity, but after the tinyness of the change using that increasing sizes, I think that this idea should be rather unlikely (I'll try the Kneser-solution later)
The values for the comparisions are

   n^n           \\ = 66.1807801442
   tet_poly(2,n) \\ = 66.1807801442

So this is one approximation using a very rough method, which I call "polynomial tetration" because using fractional powers by diagonalization of a finite Carleman matrix this involves to find roots of (finite) polynomials.

Alternatives known to me:

  • In the tetration-forum one can find a procedure which extends Hellmuth Kneser's method, which was developed for basis $e\approx 2.718$ to other bases, which would give a very similar result, (search in the tetrationforum for "Sheldon Levenstein" and "fatou.gp" for a Pari/GP-procedure) By some experiments it seemed that the polynomial method converges to that so-generalized Kneser-method when the polynomial method could use matrices of infinite size, so the above result is possibly much meaningful/appropriate.

  • One different, fairly well known method, is based on E. Schröder's method, finding the "Schröder-function" $\sigma()$ first and do the fractional part of the tetratrion based on this function. Unfortunately $\sigma()$ has then complex coefficients because the tetration-base $2$ has only complex fixpoints. I didn't try such a solution at the moment.

  • Also I could not test the - (self-claimed to be) best- proposal for the tetration to fractional heights developed by D.Kousnetzov & H.Trappmann (the latter is the founder of the "tetration-forum") . I didn't see a peer-reviewed edition so far, maybe meanwhile it exists. At least it can be downloaded from arXiv, but I were unable to (re-) implement the procedure to do own computations. See the link to the Kousnetzov/Trappmann -paper in the reference-section in the wikipedia-entry for tetration. Also see the longer and more detailed entry in the citizendium

Papers on arXiv

  • R. Aldrovandi explaining and using Carleman matrices for tetration

  • D.Kouznetsov,H.Trappmann explaining their tetration-proposal in the case of two complex fixpoints (which would fit here with the base $b=2$)

A draft paper initially for the discussion in the tetration-forum on my own webspace:

  • G.Helms how different a couple of methods look in a graphical comparision (I used for the example base $b=4$ but I think it gives an idea for the caveats if one decides for one of the methods)
Gottfried Helms
  • 34,920
  • 2
    3.4141760984020147407016 so definitely not $\sqrt{2}+2$. There is also a solution at zero; however $n^n$ has a singularity at n=0. One can graph the two functions ... also it is interesting to consider other tetration bases other than b=2 for $x^x = \text{Tet}_b(x)$ – Sheldon L Oct 20 '16 at 13:23
  • 1
    @Sheldon - nice to see more digits; I didn't get your last fatou.gp not working for base 2, and hat no time to search for the tiny bug... (maybe some unlucky interference with my default-loaded library of standard functions). What I've done was to look at the similar question with base $3$ instead of $2$ for the $;^n 3$ and $n^{n^n} = ;^3 n$ instead of $ ; ^2 n$ . The nontrivial solution was near the other solution, and may be gives a nice game by generalization ... :-) – Gottfried Helms Oct 20 '16 at 14:47
  • 1
    Since Fatou.gp is a "complex base" program, for the Abel/slog which needs to be inverted to get the sexp, it may be that fatou.gp is returning results with $\Im(z)=0$. – Sheldon L Oct 21 '16 at 14:52
  • 1
    Hi @Sheldon, I got it working with the older version "tetcomplex.gp" and found that number which you've provided. (Just small adaptions to avoid name-conflicts with the variables and functions of my standard functions-lib.) – Gottfried Helms Oct 25 '16 at 12:05
2

I wanted to add some graphs to Gottfried's solution. First definitions; $\text{sexp}_2(z)= \;^z 2$ which is extended to the complex plane by Kneser's solution. I wrote a program to calculate the slog; which is the inverse of sexp and has some nice uniqueness properties. The fatou.gp program works for a wide range of real and complex sexp bases and is written in pari-gp and is available on this site http://math.eretrandre.org/. Instead of graphing $\text{sexp}_2(x)\;$and $\;x^x$, I will take the $\log_2(x)$ of both equations which works when both are positive. So I am graphing $$\text{sexp}_2(x-1)\;\;\text{vs}\;\;\log_2(x^2)=\frac{x\ln(x)}{\ln(2)}$$

Here is a graph for sexp base 2 which shows a solution at x=0, x=2, and at x=3.4141760984020147407016 sexp base 2

What about other bases? Here is a graph for sexp base=2.1150455841, which has a parabolic crossing near 2.5360 so there are only two solutions. sexp2.115

For larger bases, there is only one solution. Here is sexp base e which only has a solution at x=0.sexp base e

Sheldon L
  • 4,534