I'm currently studying in Grade 8 and I took a huge interest in math. I'm still learning algebra and I was currently wondering if I could start at least the most basic concepts of calculus. I have not taken trigonometry and I was just wondering. Is it possible or is it too early for me? PS: This is my first question here! Thank you!
4 Answers
Here's the online notes I personally used to get through Calculus. I will note that it requires Algebra, so you definitely need to be comfortable with the subject. As a hint at what Calculus is like, consider the following:
$$y=\frac{x^2-1}{x-1}$$
Most likely you will be faced with the question "What is $y$ when $x\approx1$?" If you plug in $x=1$, you will get division by $0$ error, but,
$$\begin{array}{c|c}x&y\\\hline0.9&1.9\\\hline0.99&1.99\\\hline1&?\\\hline1.01&2.01\\\hline1.1&2.1\end{array}$$
You can get a good picture of what the answer is, but Calculus will make this concept rigorous with algebra and limits, which is the first topic. The answer to the above question is indeed $y=2$.
Trigonometry is rather simple as far as definitions:
Those are the basic formulas of trigonometry. You should already know a fourth equation:
$$a^2+o^2=h^2$$
Such simple triangles will get increasingly complicated in how you will use them, but it is good to know what they are, which isn't too much at all. Just draw some triangles, find the side lengths, and you get $\sin,\cos,\tan$.
There is a topic in Algebra that I want to make note of, and you should be coming close to it. It is complex numbers. See that
$$x^2-1=(x-1)(x+1)$$
But there is no such normal solution to
$$x^2+1=(x+?)(x+?)$$
If we let such a number exist, it shall have to be $i=\sqrt{-1}$, which is quite absurd, but anyways,
$$x^2+1=(x+i)(x-i)$$
You may ask what this has to do with any of the above, and I will simply tell you there are connections between this and triangles, and secondly, that if you allow such numbers, calculus can be easier sometimes.
To give you the connection, take $1+i$. Then draw it on a complex plane. Then take $(1+i)^2$ and draw it on the graph. Same with $(1+i)^3$ etc. etc. until you feel satisfied. Then, will you be able to see any triangles? Mainly, can you find triangles that start from $(0,0)$ and connect to each point? What can you deduce about angles?
Then ask if it is reasonable to take the Algebra path to find $(1+i)^{100}$ or to use triangles.
Now, if you happen to be interested in coding, I recommend numerical analysis. As a sneak peak:
Find $\sqrt2$ in decimal form:
$$a_0=1\\a_1=\frac{(a_0)^2+2}{2\times a_0}=\frac32=1.5\\a_2=\frac{(a_1)^2+2}{2\times a_1}=\frac{17}{12}=1.41666\\a_3=\dots=\frac{577}{408}=1.41421$$
Which is equivalent to $\sqrt2$ out 5 decimal places. If you keep doing this forever, you will get $\sqrt2$ out as many decimals you desire. Best done with a program.
I will also recommend finishing Algebra early. Find a book to read so that you can get a good head start.
Discrete mathematics are also a good place. An example of something simple:
$$1+2+3+\dots+n=\frac{n(n+1)}2$$
I personally find the topic interesting, and it connects to calculus in some ways.
- 74,685
Learn basic facts about quadratic equations, solving them, roots of polynomials, multiplying and dividing polynomials with remainders. And definitely trigonometry. In a strict sense trigonometry is unnecessary for development of calculus, but knowing that well is a huge plus and recommended.
Also basic things about two-dimensional analytic (co-ordinate ) geometry: equations of lines, circles, parabolas their tangents.
These will provide you enough examples, and enough problems to practice in calculus.
- 19,504
Ok, I had faced a very similar situation years back, here's my advice for you.
If you start studying basics of Calculus from $8th$ grade itself, that won't be problem. But you'll encounter a situation where you would need to deal with trigonometric and logarithmic functions, especially the former one. So be sure you study the basics, and if you don't, you'll have to return there definitely someday.
If you still have the interest, try the book Calculus for Dummies , that will provide you a nice mental platform for further studies.
Solve as much problems as possible. Calculus is vast, and encapsulates much of math, be sure to prepare early and smart.
Book Recommendations:
- SL Loney, Trigonometry.
- Hall and Knight, Higher Algebra.
- Problems in Mathematics, Govorov.
Best of luck!
- 1,079
-
Thanks! I'll probably study more algebra and trigonometry since I've only started quadratic equations and simplifying quadratic expressions. – galaxymcpvp Oct 16 '16 at 14:55
-
1
-
1@SimpleArt He said he's learning Algebra, so he doesn't need it, probably. – Das Oct 16 '16 at 14:57
-
@SwapnilDas Didn't see his comment by the time I finished my comment. And its still good to finish Algebra early before Calc. – Simply Beautiful Art Oct 16 '16 at 14:58
Perhaps you'd be better off learning your current curriculum first. I was in the exact same position in 8th grade ( for physics though; I wanted to learn tensor analysis in order to tackle general relativity...finally did it in 10th :)), and I learnt this the hard way.Reason- Math is pretty vast. When you really reach a position to pursue the more intricate details, you will need to choose between the many branches it offers(say, topology or number theory); and in order to really realise what you ACTUALLY want, you should be in a better position to appreciate all of them. I would suggest that right now you focus more on building your intuition rather than romping through textbooks. If I may, I'd like to suggest a few books you can use, preferably in the SAME order.
Hall and Knight - Higher Algebra
SL Loney-Trigonometry; Coordinate geometry
IA Maron- Calculus of one variable
David M Burton-Number theory ( one of my favourites)
Walter Rudin - Mathematical analysis ( Goldberg works too)
Coddington- Ordinary differential equations
Gillespie- Partial differentiation
Widder - Advanced calculus
Phew! But don't get overwhelmed; this will require at least 2-3 years, so take it one step at a time. This was just to give you a ready reference and show you how vast math really is...any questions, fire away!
Hope this helps
- 589
- 1
- 6
- 16
-
Thanks! I also like physics especially quantum mechanics and that is why I was asking requirements for calculus. – galaxymcpvp Oct 16 '16 at 15:50
-
Good to know....just so you know, Griffith's book on quantum electrodynamics and quantum mechanics are pretty cool...especially for beginners. But go through Feynman lectures first-my all time favourites :) – GRrocks Oct 16 '16 at 15:52
-
@galaxymcpvp Good luck good sir. Learn all the things for your dreams and be the 16 year old quantum mechanic! – Simply Beautiful Art Oct 16 '16 at 23:54
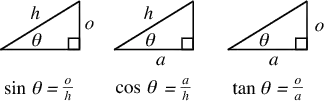
(algebra-precalculus)tag. – Simply Beautiful Art Oct 16 '16 at 14:51