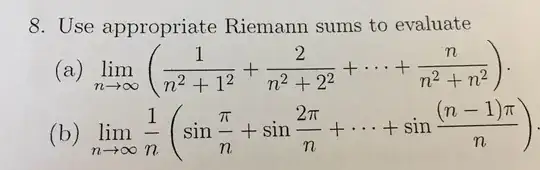
Not sure how to get started on this question. Do I have to form the summation? If yes, how do I go about doing it? Any help will be really appreciated!
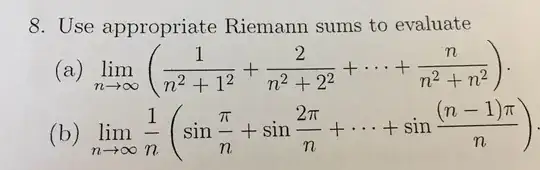
Not sure how to get started on this question. Do I have to form the summation? If yes, how do I go about doing it? Any help will be really appreciated!
Hint: For a) we have \begin{align} \lim_{n\rightarrow \infty}\sum^n_{k=1} \frac{k}{n^2+k^2}= \lim_{n\rightarrow \infty}\sum^n_{k=1} \frac{k/n}{n(1+k^2/n^2)} = \int^1_0 \frac{x}{1+x^2}\ dx. \end{align} Likewise, we can expression b) as an integral \begin{align} \int^1_0 \sin \pi x\ dx. \end{align}