Does the sum $\sum_{n \geq 1} \frac{2^n\operatorname{mod} n}{n^2}$ converge?

Question

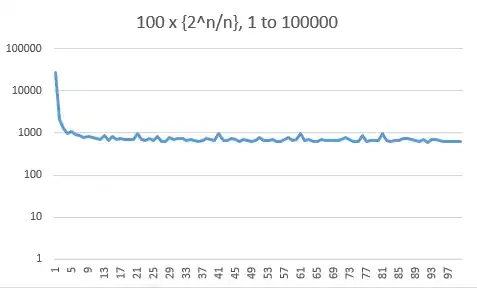
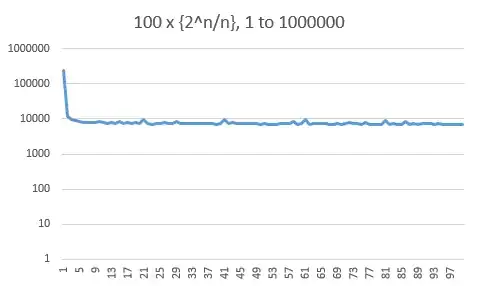
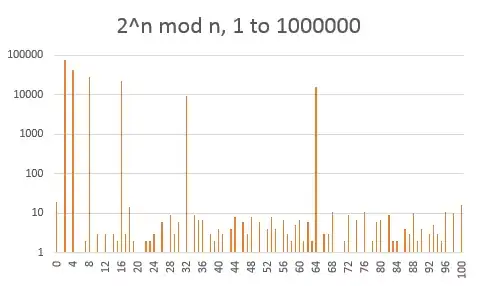
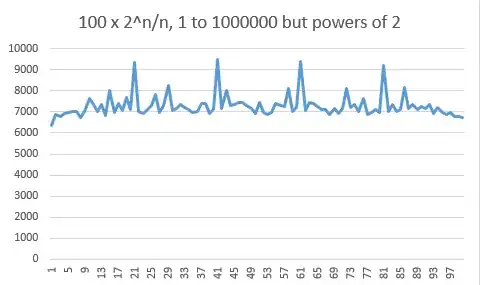
I am somewhat a noob, and I don't recall my math preparation from college. I know that the sum $\displaystyle \sum_{n\geq 1}\frac{1}{n}$ is divergent and my question is if the sum$$\sum \limits _{n\geq 1}\frac{2^n\mod n}{n^2}$$converges. I think is not but I do not know how to prove that! Thanks!

Answer 1

In this answer, we prove that

$$ \sum_{n=1}^{\infty} \frac{2^n \text{ mod } n}{n^2} = \infty. \tag{*} $$

---

Idea. The intuition on $\text{(*)}$ comes from the belief that the sequence $(2^n \text{ mod } n)/n$ is equidistributed on $[0, 1]$, which is quite well supported by numerical computation.

Proving this seems quite daunting, though, so we focus on a particular subsequence which is still good to give a diverging lower bound of $\text{(*)}$. To be precise, we focus on the indices of the form $n = 5p$ for some prime $p$ and prove that the corresponding sum is comparable to the harmonic series for primes $\sum_p \frac{1}{p}$, which also diverges.

---

Proof. To this end, we consider the sequence $(a_k : k \geq 0)$ in $[0, 1)$ defined by

$$ a_k = \left\{ \frac{2^{5p_k}}{5p_k} \right\},$$

where $\{ x \} = x - \lfloor x \rfloor$ is the fractional part of $x$ and $p_k$ is the $k$-th prime number. Now focusing only on the index $n = 5p_k$ for some $k$, we can bound the sum $\text{(*)}$ below by

$$ \sum_{n=1}^{\infty} \frac{2^n \text{ mod } n}{n^2} = \sum_{n=1}^{\infty} \frac{1}{n}\left\{ \frac{2^n}{n} \right\} \geq \sum_{k=1}^{\infty} \frac{a_k}{5p_k}. $$

So it suffices to prove that this bound diverges. First, for any prime $p$ we have

$$ 2^{5p} \equiv 2^5 \equiv 32 \pmod{p}. $$

This allows us to write $2^{5p} = mp + 32$ for some non-negative $m$. Next, notice that any prime $p$ other than $2$ and $5$ are either of the form $p = 4k+1$ or of the form $p = 4k+3$. Depending on which class $p$ falls in, we find that

$$ 2^{5p} \equiv 2^p \equiv \begin{cases} 2, & \text{if } p =4k+1 \\ 3, & \text{if } p =4k+3 \end{cases} \pmod{5}. $$

What this tells about $m$ is as follows:

$$ m \equiv \begin{cases} 0, & \text{if } p =4k+1 \\ p^{-1}, & \text{if } p =4k+3 \end{cases} \pmod{5}. $$

(Here, $p^{-1}$ is the multiplicative inverse of $p$ modulo $5$.) From this, for $p_k > 32$ we have the following estimate:

$$ a_k \geq \frac{1}{5} \quad \text{if } p_k \equiv 3 \pmod{4}. $$

Consequently, by the PNT for arithmetic progression,

$$ \frac{a_1 + \cdots + a_n}{n} \geq \frac{1}{5} \frac{\pi_{4,3}(p_n) + \mathcal{O}(1)}{\pi(p_n)} \xrightarrow[n\to\infty]{} \frac{1}{10}. $$

(The $\mathcal{O}(1)$-term appears by discarding terms with $p_k \leq 32$.) Finally, let $s_n = a_1 + \cdots + a_n$. Then by summation by parts, as $N \to \infty$ we have

\begin{align*} \sum_{k=1}^{N} \frac{a_k}{5p_k} &= \frac{1}{5} \bigg( \frac{s_N}{p_N} + \sum_{k=1}^{N-1} \left( \frac{1}{p_k} - \frac{1}{p_{k+1}} \right) s_k \bigg) \\ &\geq \frac{1}{5} \sum_{k=1}^{N-1} \left( \frac{1}{p_k} - \frac{1}{p_{k+1}} \right) \frac{k}{11} + \mathcal{O}(1) \\ &\geq \frac{1}{55} \sum_{k=1}^{N} \frac{1}{p_k} + \mathcal{O}(1). \end{align*}

Taking $N \to \infty$, this series diverges by the harmonic series for primes. Therefore the claim $\text{(*)}$ follows. ////

---

Elaborating this argument, we find that

$$ a_k \equiv \frac{2^{5p_k}}{5p_k} \equiv \tilde{a}_k + \frac{32}{5p_k} \pmod{1} $$

where $\tilde{a}_k$ satisfies

$$ \tilde{a}_k = \begin{cases} 0, & \text{if } p_k \equiv 1, 9, 13, 17 \pmod{20} \\ 1/5, & \text{if } p_k \equiv 11 \pmod{20} \\ 2/5, & \text{if } p_k \equiv 3 \pmod{20} \\ 3/5, & \text{if } p_k \equiv 7 \pmod{20} \\ 4/5, & \text{if } p_k \equiv 19 \pmod{20} \end{cases}. $$

Thus by the PNT for arithmetic progression again, we have the following convergence in distribution:

$$ \frac{1}{n} \sum_{k=1}^{n} \delta_{a_k} \xrightarrow{d} \frac{1}{2}\delta_{0} + \frac{1}{8}\sum_{j=1}^{4} \delta_{j/5} \quad \text{as } n \to \infty$$

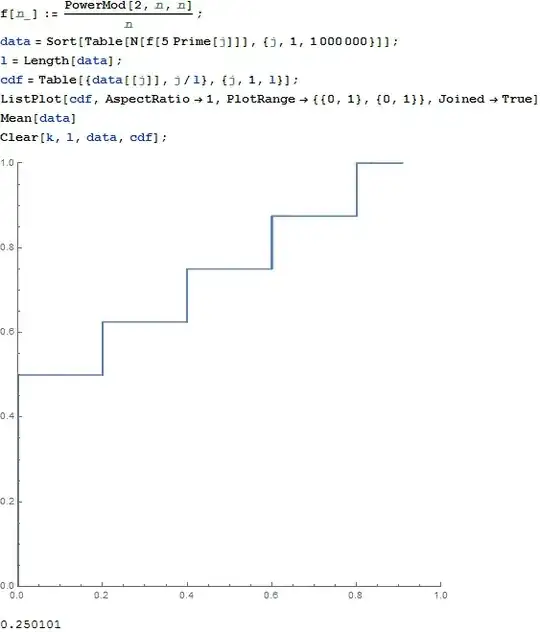
The following numerical simulation using first 1,000,000 terms of $(a_k)$ clearly demonstrates this behavior:

Answer 2

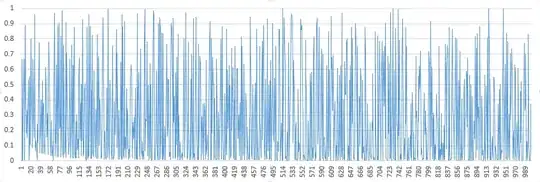
Not an answer, just for insight. Here is a plot of the $1000$ first $\dfrac{2^n\mod n}n$, to substantiate the "uniform distribution" hypothesis.

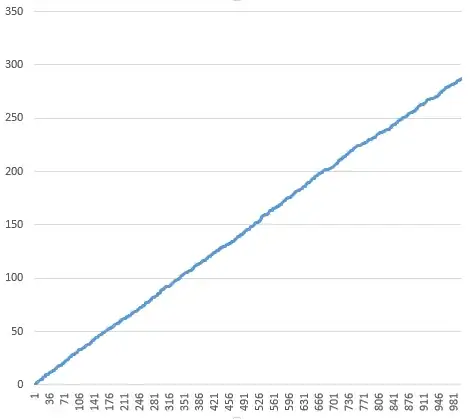
The second plot is the prefix sum, which is a straight line for a uniform distribution. The average of the values is $0.287$ (not very close to $0.5$).

Unfortunately, this empirical data isn't sufficiently conclusive.

---

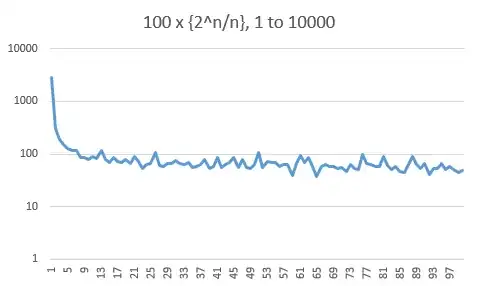
Here are histograms of the fractional part of the $10000$, $100000$ and $1000000$ first values. Beware that the frequency axis is logarithmic. There is a strong bias towards the small values (one third below $0.01$), but this doesn't seem to worsen with $n$.

I conjecture that for any $n$, at least $50\%$ of the values of $\{2^k/k\}$ are above $0.1$.

Very interestingly, the histogram of the values $2^n\bmod n$ themselves shows very strong lines for all powers of $2$.

This leads us to the next histogram, where the moduli that are powers of $2$ have been ignored. There is no more need for a logarithmic scale and the distribution looks pretty flat now.

Answer 3

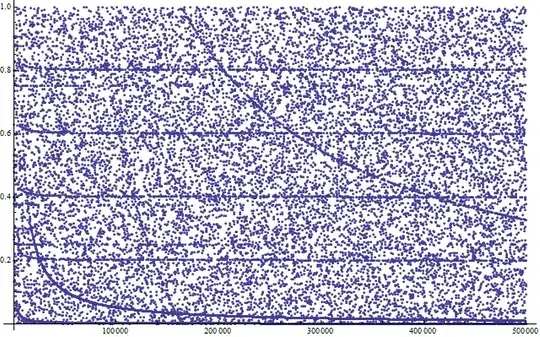
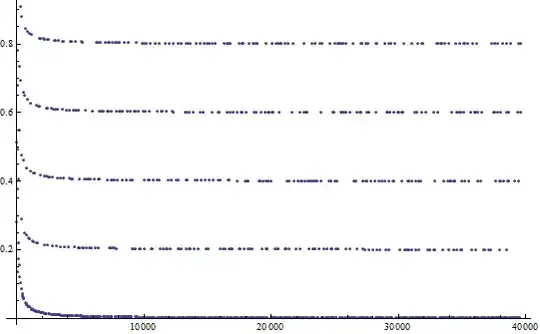
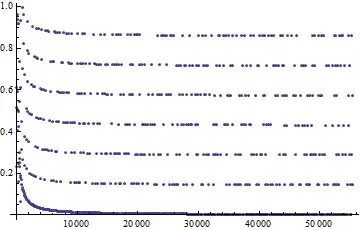
The point of this post is to give some plots that corroborate Sangchul Lee's argument. These were produced by Mathematica

The first plot lists the numbers $(2^n\mod n)/n$ for all multiples of $5$. You see the horizontal lines at multiples of $0.2$. They were already visible in the unrestricted plot, when I didn't restrict $n$ to multiples of five, but here they are easier to spot:

When we only include the values $n=5p$, the picture is even clearer:

Multiples of five are not the only structure in there. Restricting the choice of $n$ to numbers of the form $n=7p$ gives something quite similar.