From Wikipedia page: Eisenstein Criterion:
I thought the irreducibility in $\mathbb Q[X]$ automatically implies the irreducibility in $\mathbb Z[X]$, because $\mathbb Z\subset \mathbb Q$.
Could someone give a counterexample of a polynomial $f\in \mathbb Z[X]$ which is irreducible over $\mathbb Q[X]$ and reducible over $\mathbb Z[X]$?
$2 x$ is such an example. If you read the article carefully, the idea is already in there.
I know it might feel a little bit like cheating, but this is what they mean: The polynomial $5x + 5$ is reducible in $\Bbb Z[X]$, but not in $\Bbb Q[X]$. The reason is that in $\Bbb Q[x]$, the factor $5$ is invertible, and therefore "doesn't count", while in $\Bbb Z[X]$, $5$ is not invertible, and therefore $5\cdot (x+1)$ is a valid reduction.
The main idea to take with you is that "reducibility" is not a property of polynomials per se, but a property of elements in any ring. An element $r \in R$ is reducible if we can find non-invertible $s, t \in R$ such that $r = st$.
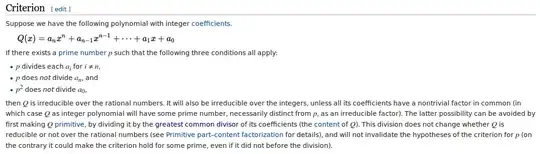
If you read that wikipedia article, they say exactly this: "(in which case $Q$ as integer polynomial will have some prime number, necessarily distinct from $p$, as an irreducible factor)"
