1

What is the joint PDF of two uniformly distributed random variables and their sum?

em70
  • 241
  • 2
    What would you like it to be? The marginal pdfs do not, in general, determine the joint pdf uniquely. For example, $f(x,y)$ could have value $1$ on the unit square, or value $2$ on two smaller squares, one with diagonally opposite corners at $(0,0.5)$ and $(0.5,1)$ and the other with diagonally opposite corners at $(0.5,0)$ and $(1,0.5)$. – Dilip Sarwate Sep 15 '12 at 00:15
  • 2
    The problem I'm trying to tackle is really finding the marginal pdf p(e,f) given that a,b,c are uniform and iid RVs while e,f are a+b and a+c respectively. No matter how I turn it around the problem seems to always require some messed up joint dist which I can't derive! – em70 Sep 15 '12 at 00:26
  • 1
    Then ask THIS question. – Did Sep 15 '12 at 06:12

2 Answers2

7

I will try to address the question you posed in the comments, namely:

Given 3 independent random variables $U$, $V$ and $W$ uniformly distributed on $(0,1)$, find the joint probability distribution function of $X=U+V$ and $Y=U+W$.

Gives $0<x<2$ and $0<y<2$, we first compute $F_{X,Y}(x,y)$: $$\begin{eqnarray} F_{X,Y}(x,y) &=& \mathbb{P}\left(X \leqslant x, Y \leqslant y\right) = \mathbb{P}\left(U+V \leqslant x, U+W \leqslant y\right) = \mathbb{E}\left(\mathbb{P}\left(U+V \leqslant x, U+W \leqslant y|U\right)\right)\\ &=& \mathbb{E}\left(F_V(x-U)F_W(y-U)\right) = \mathbb{E}\left(\min(1, \max(x-U,0))\min(1, \max(y-U,0))\right) \end{eqnarray} $$ The pdf, being a derivative of the cdf, will then read: $$ f_{X,Y}(x,y) = \frac{\partial}{\partial x} \frac{\partial}{\partial y} F_{X,Y}(x,y) = \mathbb{E}\left( [1+U>x>U] [1+U > y>U] \right) = \mathbb{P}\left(U < x < 1+U \land U < y<1+U\right) $$ The evaluation of the latter expectation is straightforward but tedious, so I asked Mathematica for help: 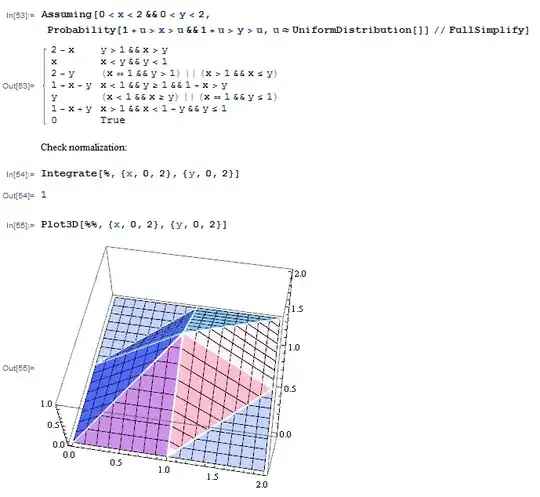enter image description here

Sasha
  • 70,631
  • Wonderful! I just have a bit of trouble following how you calculate the partial derivatives of the CDF (keeping things so neat!) – em70 Sep 15 '12 at 13:57
  • 1
    Well, you could have done as $$\partial_x \partial_y \mathbb{E}\left(F_V(x-U) F_W(y-U) \right) = \mathbb{E}\left(f_V(x-U) f_W(y-U) \right) = \mathbb{E}\left([0<x-U<1] \cdot [0<y-U<1 ] \right) $$ – Sasha Sep 15 '12 at 14:11
  • +1 - just what I needed. I awarded, for fairness, the answer to did, however, as that is the correct answer to the question – em70 Sep 15 '12 at 17:01
2

The problem I'm trying to tackle is really finding the marginal pdf p(e,f) given that a,b,c are uniform and iid RVs while e,f are a+b and a+c respectively.

Call $X=U+V$ and $Y=U+W$ for $(U,V,W)$ i.i.d. uniform on $(0,1)$. The common density of $U$, $V$ and $W$ is $\mathbf 1_{(0,1)}$ hence the density of $(X,Y)$ is the function $f$ defined by $$ f(x,y)=\int_0^1\mathbf 1_{(0,1)}(x-u)\,\mathbf 1_{(0,1)}(y-u)\,\mathrm du. $$ Introducing $s=\min(x,y)$ and $t=\max(x,y)$, this is $f(x,y)=s$ if $0\lt s,t\lt1$ and $f(x,y)=s-t+1$ if $1\lt t\lt2$ and $t\lt1+s$.

Did
  • 279,727