I have this image
I know the real width of the road (green color, for example 2 meters) and the length of the road between two green lines in the background (orange, for example 3 meters). Is it possible to measure how long would be the red line on paper/pc in cm/pixels, if I want it to be 3 meters in real life, just from the stated information?
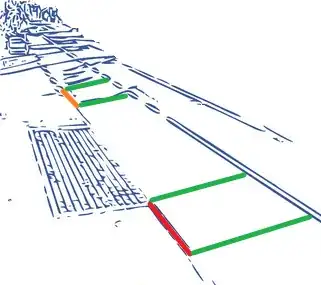
I'm showing below a geometrical way to find what you want. Let $A$, $B$, $C$, $D$ be the endpoints of red and orange line segments in your picture, and let $O$ be the vanishing point where line $ABCD$ intersects the other side of the road.
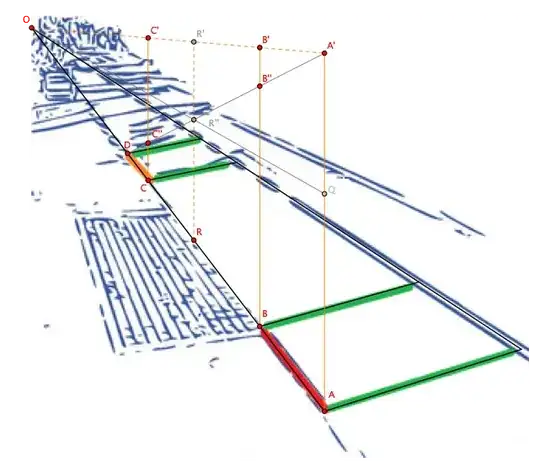
Draw from $A$, $B$, $C$ three parallel lines and choose on them points $A'$, $B'$, $C'$, aligned with $O$. Join $A'D$ and let $B''$, $C''$ be the points where line $A'D$ intersects $BB'$ and $CC'$. You can see in the diagram below how these lines would appear in reality. Notice that lines $AA'$, $BB'$ and $CC'$ are parallel between them and to the view plane: that implies that all ratios of segments belonging to the same line have the same value both in reality and in the picture.
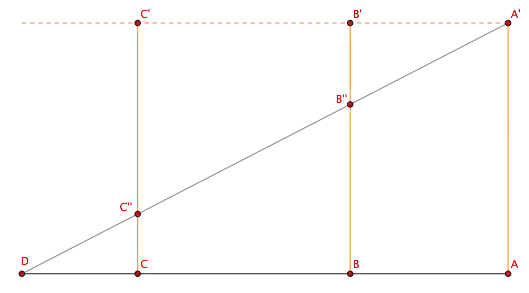
By similar triangles it is then easy to find the following relation among real lengths: $$ {AB\over CD}\cdot{CC''\over CC'}=1-{BB''\over BB'}. $$
But ${CC''\over CC'}$ and $BB''\over BB'$ can also be measured from the picture, so you can find that $AB/CD\approx 0.53$ and $AB$ is then slightly more than 1 meter.
To find a point $R$ on $ABCD$ such that $AR/CD$ has a given value, you can rewrite the above relation as $$ {RR''\over RR'}=1-{AR\over CD}\cdot{CC''\over CC'} $$ and notice that if $Q$ is the intersection between line $OR$ and $AA'$, then ${RR''\over RR'}={AQ\over AA'}$. You can then construct point $Q$ on $AA'$ such that ${AQ\over AA'}=1-{AR\over CD}\cdot{CC''\over CC'}$ and find $R''$ as the intersection between $QO$ and $A'D$. From that it is easy to find point $R$: in the above picture, point $R$ was constructed so that $AR/CD=3/2$, as you required.
One way to do this is to find a planar perspective transformation that maps between image and world coordinates for the known quadrilateral (green/orange). Once you have that transformation, you can use it to map the endpoints of any line segment in the image back to world coordinates and so get the “real world” length of the segment.
This computation is available in many graphics library APIs, but if you have to do it yourself, I describe a method in my answer to this question.
Clarification: I should say that you can measure any line segment known to be in the plane of the road this way. Mapping back to arbitrary points on the 3-D world is harder.
