1

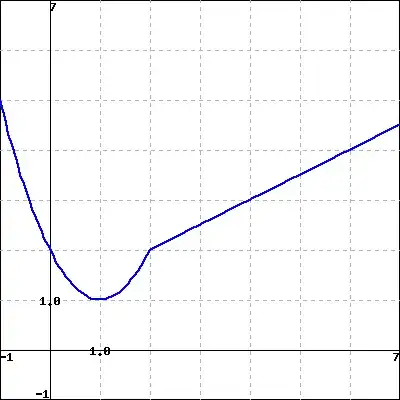
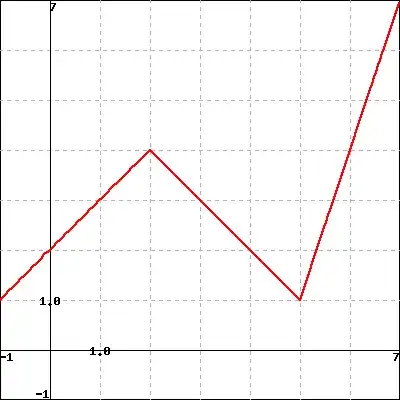
The graphs of the function $F$ (left, in blue) and $G$ (right, in red) are below. Let $P(x)=F(x)G(x)$ and $Q(x)=F(x)/G(x)$.

Answer the following questions.

  1. $P′(1)=$
  2. $Q′(1)=$
  3. $P′(6)=$
  4. $Q′(6)=$

Here is the graph of $y=F(x):$

enter image description here

And here is the graph of $y=G(x):$

enter image description here

I know this is asking me to be able to use the Product and Quotient rule to find the derivatives; Product rule if asking for $P'(x)$ and Quotient for $Q'(x)$. I am fairly okay with doing these two. However, I am unsure how to get the numbers I need from the graph: the $f(x), g(x)$, $f'(x)$ and $g'(x)$. I believe $f(x)$ would be $1$ and $g(x)$ would be $3$, but I am unsure--and definitely unsure about how to get the $f'(x)$ and $g'(x)$. Any help would be appreciated.

Rory Daulton
  • 32,288
Nadia Serpentis Perry
  • 21
  • It would be worth mentioning what attempts to have made to find the derivatives, and then we can pick up from where you got stuck. Also would I be correct in assuming that the left hand side of the blue figure is a quadratic? – oliversm Oct 07 '16 at 22:49
  • https://math.stackexchange.com/a/4261764/945479 – qifeng618 Sep 28 '21 at 01:49
  • https://math.stackexchange.com/a/4261705/945479 – qifeng618 Sep 28 '21 at 01:51

2 Answers2

1

Since you are asked for $P'(x)$ at both $1$ and $6$, and the same for $Q'(x)$, you need to be more clear as to the values of $x$. Here is what I read straight from the graphs:

$$F(1)=1, \quad F(6)=4$$ $$G(1)=3, \quad G(6)=4$$

The derivatives are only slightly more tricky: look at the slope of the tangent line.

$$F'(1)=0, \quad F'(6)=\frac 12$$ $$G'(1)=1, \quad G'(6)=3$$

Rory Daulton
  • 32,288
  • After I asked the question initially, I was able to see why F' = 0, G' = 1, etc. Do I then need to use these numbers to solve for P'(1)? When I originally read the problem, and I have it here as it's shown for me, that I would need to do the Product rule and Quotient rule (depending on if it's asking for P' or Q'). – Nadia Serpentis Perry Oct 08 '16 at 00:01
  • @NadiaSerpentisPerry: Since $P(x)=F(x)\cdot G(x)$, then $P'(1)=F'(1)\cdot G(1)+F(1)\cdot G'(1)$, and similarly for the other problems. That is directly from the product rule, using $x=1$. – Rory Daulton Oct 08 '16 at 00:30
  • I see what the problem was. I had the wrong value when I tried to get the slope of the tangent line for F. I was doing the product and Quotient rule correctly, but with one incorrect number. :/ I guess I will have to refresh myself on finding the slope of the tangent line if it's a curve. – Nadia Serpentis Perry Oct 08 '16 at 00:49
0

The only values of interest for your calculation are P'(1),P'(6),Q'(1) and Q'(6). You dont need to be able to get the derivative for any possible x. So how do you get these four?
P'(1) seems to be a turning point. Therefore, the derivative has to equal 0 in this spot.
The other three derivatives are all within a linear segment. To get the derivative here, you just need to calculate the rise of that segment, divided by the length.
For P'(6) the line goes one box up for two boxes to the right. So P'(6)= 1/2 = 0.5. The same way you get Q'(1)= 1 and Q'(6) = 3.

Syntac
  • 1