1

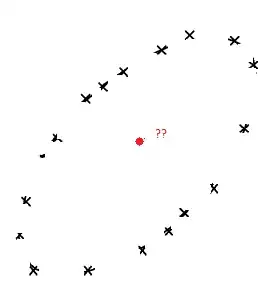
I am trying to figure out if any given pixel is inside a region which is defined by other pixels, not a formula. In my case the pixels that define the region come from a projected ellipsoid, I could not find a formula that would allow me to run the test in 2D, so I have to run the test numerically. However the pixels that define the region have gaps - what to do in this situation? Should I interpolate in 2D, and shoot off rays in 4 directions to check intersections, or is there a more elegant approach?

enter image description here

BBSysDyn
  • 16,115
  • 4
    If the region is convex, then compute $(x-p_n)\times(p_{n+1}-p_n)$ for all corner points $p_n$; if the result has the same sign for every $n$, $x$ is within the region. – hmakholm left over Monica Oct 06 '16 at 14:38
  • 1
    As the points in your diagram appear to lie in an ellipse you could find its equation then directly compare it. As it stands at the moment you only have an implied area and computers aren't good with assumptions like that. – Ian Miller Oct 07 '16 at 00:50
  • @HenningMakholm I tested, it works! Thanks. I believe the math is related to this answer - http://math.stackexchange.com/a/190203/6786 – BBSysDyn Oct 07 '16 at 06:27

1 Answers1

1

Per @HenningMakholm's answer:

pts = [[182,250],[153,278],[149,309],[168,336],[198,309],[205,280],[198,263]]
pts = np.array(pts)
pt1 = np.array([180,280]) # inside 
a = pts - pt1
aa = a[:len(d),:]
d = np.diff(pts,axis=0)
print np.cross(aa,d)
pt2 = np.array([380, 280]) # outside
a = pts - pt2
aa = a[:len(d),:]
print np.cross(aa,d)
BBSysDyn
  • 16,115