6

I've heard that $1+1/4+1/9+1/16+1/25+...$ converges to $\pi^2/6$. This was very surprising to me and I was wondering if there was a reason that it converges to this number?

I am also confused why $\pi$ would be involved. If someone could provide a proof of this or a intuitive reason/ derivation I would appreciate it. I am only able to understand high school maths however (year 12).

Martin Sleziak
  • 53,687
Simon
  • 291
  • 9
    This may interest you: http://math.stackexchange.com/questions/8337/different-methods-to-compute-sum-limits-k-1-infty-frac1k2 – Augustin Oct 05 '16 at 08:29
  • This was the famous "problem of Basilea", what makes that a young Euler was recognized internationality as a great mathematician. – Masacroso Oct 05 '16 at 08:40
  • 1
    Unfortunately, it's impossible to understand this without at least a little bit of fairly heavy machinery, and also some amount of patience. Often it is the case in mathematics that you can trade one for the other, but only up to a point. I think that Pedro Tamaroff's answer is the closest I've ever seen to the "no machinery all patience" side of that spectrum. (But even this requires Taylor's theorem, and either an understanding of or belief in termwise integration of a series) – Eric Stucky Oct 05 '16 at 08:44
  • 1
    The most interesting proof is with $\cot(z) =\lim_{N \to \infty} \sum_{n=-N}^N \frac{1}{z-\pi n}$ , that's what made Euler truly famous – reuns Oct 05 '16 at 08:46
  • Understanding the deep "why $\pi$ appears" remains a different and interesting question. IMO, a real answer is "because $\pi$ is a root of the sine function" and the Basel problem is just another way to formulate that, an alternative being by the Gregory series. –  Oct 05 '16 at 10:01
  • Regarding the involvement of $\pi$ I would recommend watching this beautiful explanation from 3blue1brown! https://youtu.be/d-o3eB9sfls – Isti115 Jul 06 '18 at 22:42

1 Answers1

8

Some of the proofs in the given link are somewhat technical and I'll try to vulgarize a variant of one of them.

Consider the function $$f(x):=\frac{\sin\pi\sqrt x}{\pi\sqrt x}.$$

This function has roots for every perfect square $x=n^2$, and it can be shown to equal the infinite product of the binomials for the corresponding roots

$$p(x):=\left(1-\frac x{1^2}\right)\left(1-\frac x{2^2}\right)\left(1-\frac x{3^2}\right)\left(1-\frac x{4^2}\right)\cdots$$

(obviously, $p(0)=f(0)=1$ and $p(n^2)=f(n^2)=0$.)

If we expand this product to the first degree, we get

$$1-\left(\frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\frac1{4^2}+\cdots\right)\,x+\cdots$$

On the other hand, the Taylor development to the first order is

$$f(0)+f'(0)\,x+\cdots=1-\frac{\pi^2}6x+\cdots$$ hence the claim by identification.

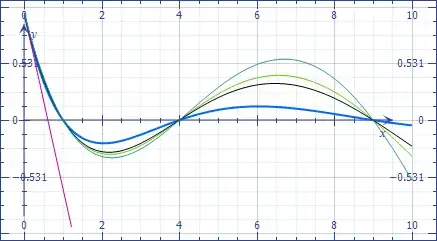
The plot shows the function $f$ in blue, the linear approximation in red, and the product of the first $4,5$ and $6$ binomials, showing that they coincide better and better.

enter image description here

  • Unfortunately, I have no rigorous proof that $p(x)=f(x)$ in some neighborhood of the origin. The product can be turned to a sum by taking the logarithm. –  Oct 05 '16 at 09:31
  • the proof is that $\cot(z) - \sum \frac{1}{z - \pi n}$ is analytic and bounded – reuns Oct 05 '16 at 09:47
  • @user1952009: okay, but this is not elementary. –  Oct 05 '16 at 09:55